
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
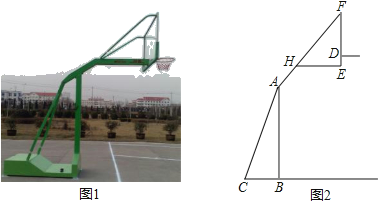
【答案】(1)45°;(2)2.75米
【解析】
(1)由cos∠FHE=![]() =
=![]() 可得答案;
可得答案;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,据此知GM=AB,HN=EG,Rt△ABC中,求得AB=BCtan60°=1.3![]() ;Rt△ANH中,求得HN=AHsin45°=
;Rt△ANH中,求得HN=AHsin45°=![]() ;根据EM=EG+GM可得答案.
;根据EM=EG+GM可得答案.
解:(1)在Rt△EFH中,cos∠FHE=![]() =
=![]() =
=![]() ,
,
∴∠FHE=45°.
答:篮板底部支架HE与支架AF所成的角∠FHE的度数为45°;
(2)延长FE交CB的延长线于M,过点A作AG⊥FM于G,过点H作HN⊥AG于N,
则四边形ABMG和四边形HNGE是矩形,
∴GM=AB,HN=EG,
在Rt△ABC中,∵tan∠ACB=![]() ,
,
∴AB=BCtan60°=1.3×![]() =1.3
=1.3![]() (米),
(米),
∴GM=AB=1.3![]() (米),
(米),
在Rt△ANH中,∠FAN=∠FHE=45°,
∴HN=AHsin45°=![]() ×
×![]() =
=![]() (米),
(米),
∴EM=EG+GM=![]() +1.3
+1.3![]() ≈2.75(米).
≈2.75(米).
答:篮板底部点E到地面的距离大约是2.75米.

故答案为:(1)45°;(2)2.75米.


科目:初中数学 来源: 题型:
【题目】某服装加工厂甲、乙两个车间共同加工一款休闲装,且每人每天加工的件数相同,甲车间比乙车间少10人,甲车间每天加工服装400件,乙车间每天加工服装600件.
(1)求甲、乙两车间各有多少人;
(2)甲车间更新了设备,平均每人每天加工的件数比原来多了10件,乙车间的加工效率不变,在两个车间总人数不变的情况下,加工厂计划从乙车间调出一部分人到甲车间,使每天两个车间加工的总数不少于1314件,求至少要从乙车间调出多少人到甲车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列4个结论:①abc<0;②2a+b=0;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论的个数是( )
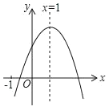
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,若![]() 点与点
点与点![]() 重合,且
重合,且![]() ,求
,求![]() 的长;
的长;
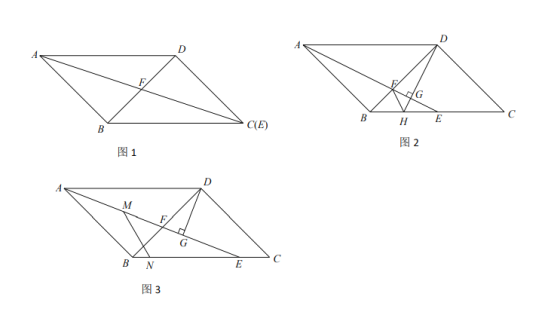
(2)如图2,当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
(3)如图3,当点![]() 在射线
在射线![]() 上运动时,过点
上运动时,过点![]() 作
作![]() 于
于![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 边上且
边上且![]() ,已知
,已知![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,∠BDC=30°,DC=4,AE⊥BD于E,CF⊥BD于F,且E、F恰好是BD的三等分点,AE、CF的延长线分别交DC、AB于N、M点,那么四边形MENF的面积是( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴相交于负半轴,给出五个结论:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤当﹣1<x<1时,y<0;其中正确的结论的序号( )
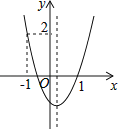
A.①③⑤B.②③④C.①③④D.②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一台实物投影仪,图2是它的示意图,折线O﹣A﹣B﹣C表示支架,支架的一部分O﹣A﹣B是固定的,另一部分BC是可旋转的,线段CD表示投影探头,OM表示水平桌面,AO⊥OM,垂足为点O,且AO=7cm,∠BAO=160°,BC∥OM,CD=8cm.
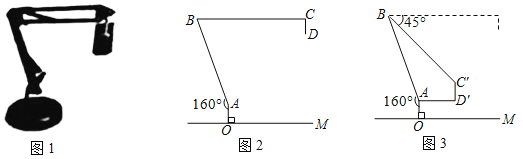
将图2中的BC绕点B向下旋转45°,使得BCD落在BC′D′的位置(如图3所示),此时C′D′⊥OM,AD′∥OM,AD′=16cm,求点B到水平桌面OM的距离,(参考数据:sin70°≈0.94,cos70°≈0.34,cot70°≈0.36,结果精确到1cm)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:我们在学习四边形的相关知识时,认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形,下面我们用尺规作图的方法来体会它们之间的联系.如图,在□ABCD中,AB=4,BC=6,∠ABC=60°,请完成下列任务:
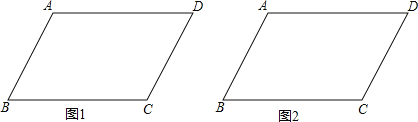
(1)在图1中作一个菱形,使得点A、B为所作菱形的2个顶点,另外2个顶点在□ABCD的边上;在图2中作一个菱形,使点B、D为所作菱形的2个顶点,另外2个顶点在□ABCD的边上;(尺规作图,保留作图痕迹,不写作法)
(2)请在图形下方横线处直接写出你按(1)中要求作出的菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学准备举办一次演讲比赛,每班限定两人报名,初三(1)班的三位同学(两位女生,一位男生)都想报名参加,班主任李老师设计了一个摸球游戏,利用已学过的概率知识来决定谁去参加比赛,游戏规则如下:在一个不透明的箱子里放3个大小质地完全相同的乒乓球,在这3个乒乓球上分别写上![]() 、
、![]() 、
、![]() (每个字母分别代表一位同学,其中
(每个字母分别代表一位同学,其中![]() 、
、![]() 分别代表两位女生,
分别代表两位女生,![]() 代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。
代表男生),搅匀后,李老师从箱子里随机摸出一个乒乓球,不放回,再次搅匀后随机摸出第二个乒乓球,根据乒乓球上的字母决定谁去参加比赛。
(1)求李老师第一次摸出的乒乓球代表男生的概率;
(2)请用列表或画树状图的方法求恰好选定一名男生和一名女生参赛的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com