
【题目】已知,在![]() 中,
中,![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() .
.
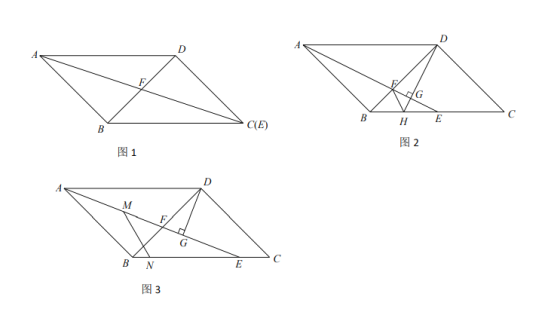
(1)如图1,若![]() 点与点
点与点![]() 重合,且
重合,且![]() ,求
,求![]() 的长;
的长;
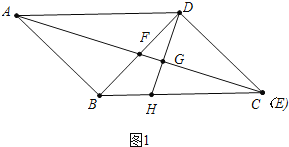
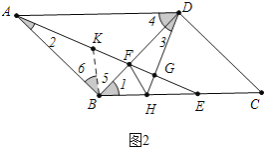
(2)如图2,当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
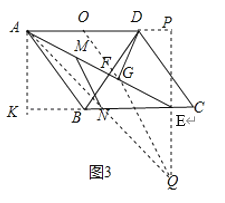
(3)如图3,当点![]() 在射线
在射线![]() 上运动时,过点
上运动时,过点![]() 作
作![]() 于
于![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 边上且
边上且![]() ,已知
,已知![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的最小值为
的最小值为![]() .
.
【解析】
(1)如图1中,利用等腰三角形的性质可得![]() ,利用平行四边形的性质可得
,利用平行四边形的性质可得![]() 为
为![]() 中点,在
中点,在![]() 中,由勾股定理可求得
中,由勾股定理可求得![]() ,则可求得
,则可求得![]() ,在
,在![]() 中,再利用勾股定理可求得
中,再利用勾股定理可求得![]() ;
;
(2)如图2中,在![]() 上截取
上截取![]() ,连接
,连接![]() ,可先证明
,可先证明![]() ,再证明
,再证明![]() ,可证得结论;
,可证得结论;
(3)连接![]() 并延长到
并延长到![]() ,使
,使![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,得到
,得到![]() ,于是得到点
,于是得到点![]() 的轨迹是以
的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的弧,且
为半径的弧,且![]() ,求得
,求得![]() 最小值为6,根据三角形的中位线定理即可得到结论.
最小值为6,根据三角形的中位线定理即可得到结论.
(1)![]()
![]()
![]()
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() 当点
当点![]() 与点
与点![]() 重合时,
重合时,![]()
在![]() 中,
中,![]()
![]()
![]()
![]() 中,
中,![]() .
.
(2)证明:如图2中,在![]() 上截取
上截取![]() ,连接
,连接![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,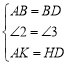 ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,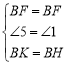 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
![]() 解:连接
解:连接![]() 并延长到
并延长到![]() ,使
,使![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() ,作AK⊥BC,交BC延长线于点K,作QP⊥AD,交AD延长线于点P.
,作AK⊥BC,交BC延长线于点K,作QP⊥AD,交AD延长线于点P.
![]() ,
,
![]() 点
点![]() 的轨迹是以
的轨迹是以![]() 为圆心,以
为圆心,以![]() 为半径的弧,且
为半径的弧,且![]() ,
,
根据△ABD为等腰直角三角形,可得AD=![]() ,
,
∴AO=![]() ,
,
根据△ABK为等腰直角三角形,可得AK=BK=4,可得QE=PE=4,
∴PQ=8,
∵BK=4,BN=1,
∴KN=5,
∴KE=AP=10,
∴OP=6,
![]() ,
,![]() ,
,
![]() 最小值为6,
最小值为6,
![]() 是
是![]() 的中位线,
的中位线,
![]() 的最小值为3.
的最小值为3.


科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
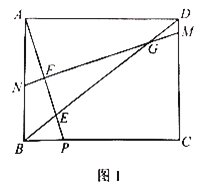
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
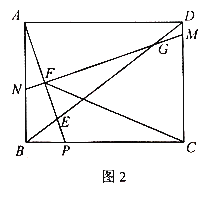
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
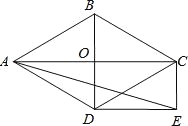
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2![]() 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
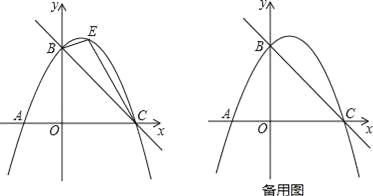
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
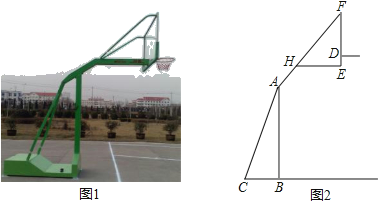
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形ABCD中,动点P从点B出发,沿折线B→C→D→B运动.设点P经过的路程为x,△ABP的面积为y.把y看作x的函数,函数的图象如图②所示,则图②中的b等于( )
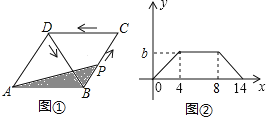
A. ![]() B.
B. ![]() C. 5D. 4
C. 5D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com