
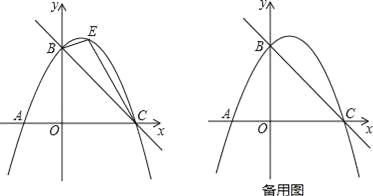
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
【答案】(1)![]() ;(2)点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3;(3)P的坐标是(﹣3,
;(2)点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3;(3)P的坐标是(﹣3, ![]() )、(5,
)、(5, ![]() )、(﹣1,
)、(﹣1, ![]() ).
).
【解析】试题分析:(1)∵直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0),∵抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,∴点B的坐标是(0,3),点C的坐标是(4,0),∵抛物线y=ax2+![]() x+c经过B、C两点,∴
x+c经过B、C两点,∴ ,解得
,解得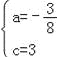 ,∴y=﹣
,∴y=﹣![]() x2+
x2+![]() x+3.
x+3.
(2)如图1,过点E作y轴的平行线EF交直线BC于点M,EF交x轴于点F,
 ,
,
∵点E是直线BC上方抛物线上的一动点,∴设点E的坐标是(x,﹣![]() x2+
x2+![]() x+3),则点M的坐标是(x,﹣
x+3),则点M的坐标是(x,﹣![]() x+3),∴EM=﹣
x+3),∴EM=﹣![]() x2+
x2+![]() x+3﹣(﹣
x+3﹣(﹣![]() x+3)=﹣
x+3)=﹣![]() x2+
x2+![]() x,∴S△BEC=S△BEM+S△MEC=
x,∴S△BEC=S△BEM+S△MEC=![]() =
=![]() ×(﹣
×(﹣![]() x2+
x2+![]() x)×4=﹣
x)×4=﹣![]() x2+3x=﹣
x2+3x=﹣![]() (x﹣2)2+3,∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(x﹣2)2+3,∴当x=2时,即点E的坐标是(2,3)时,△BEC的面积最大,最大面积是3.
(3)在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形.
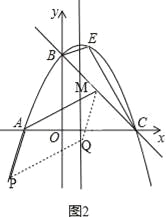
①如图2,
 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是: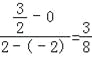 ;∵y=﹣
;∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 ,解得
,解得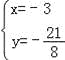 或
或 ,∵x<0,∴点P的坐标是(﹣3,﹣
,∵x<0,∴点P的坐标是(﹣3,﹣![]() ).
).
②如图3,
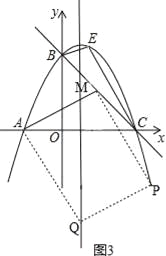 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∴AM所在的直线的斜率是:
,∴AM所在的直线的斜率是: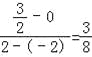 ;∵y=﹣
;∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则 ,解得
,解得 或
或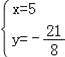 ,∵x>0,∴点P的坐标是(5,﹣
,∵x>0,∴点P的坐标是(5,﹣![]() ).
).
③如图4,
 ,
,
由(2),可得点M的横坐标是2,∵点M在直线y=﹣![]() x+3上,∴点M的坐标是(2,
x+3上,∴点M的坐标是(2,![]() ),又∵点A的坐标是(﹣2,0),∴AM=
),又∵点A的坐标是(﹣2,0),∴AM=![]() =
=![]() ,∵y=﹣
,∵y=﹣![]() x2+
x2+![]() x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣
x+3的对称轴是x=1,∴设点Q的坐标是(1,m),点P的坐标是(x,﹣![]() x2+
x2+![]() x+3),则
x+3),则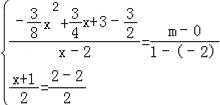 解得
解得 ,∴点P的坐标是(﹣1,
,∴点P的坐标是(﹣1,![]() ).综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣
).综上,可得在抛物线上存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形,点P的坐标是(﹣3,﹣![]() )、(5,﹣
)、(5,﹣![]() )、(﹣1,
)、(﹣1,![]() ).
).


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】请阅读下列材料:问题:现有5个边长为1的正方形,排列形式如图甲,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形. 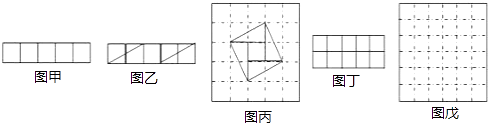
小东同学的做法是:设新正方形的边长为x(x>0),依题意,割补前后图形的面积相等,有x2=5,解得x= ![]() 由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图乙所示的分割线,拼出如图丙所示的新的正方形.
请你参考小东同学的做法,解决如下问题:
现有10个边长为1的小正方形,排列形式如图丁,请把它们分割后拼接成一个新的正方形.要求:在图丁中画出分割线,并在图戊的正方形网格图(图中的每一个小正方形的边长均为1)中用实线画出拼接成的新正方形.
说明:直接画出图形,不要求写分析过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
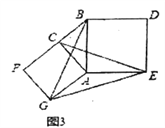
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,命题p:“B≠60°“,命题q:“△ABC的三个内角A,B,C不成等差数列“,那么p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABE和等边△ACD,连接BD,CE,试猜想BD与CE的大小关系,并说明理由.
【深入探究】
(2)如图2,△ABC中,∠ABC=45°,AB=5cm,BC=3cm,分别以AB、AC为边向外作正方形ABNE和正方形ACMD,连接BD,求BD的长.
(3)如图3,在(2)的条件下,以AC为直角边在线段AC的左侧作等腰直角△ACD,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
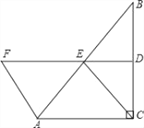
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.
(1)求证:四边形ACEF是平行四边形;
(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,延长平行四边形ABCD的边DC到点E,使CE=DC,连接AE,交BC于点F,连接AC、BE.
(1)求证:BF=CF;
(2)若AB=2,AD=4,且∠AFC=2∠D,求平行四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com