
����Ŀ����ͼ1�����ǰѶԽ����ഹֱ���ı��ν��������ı��Σ�

(l)�������⣺��ͼ2�����ı���ABCD�У�AB=AD��CB=CD�����ı���ABCD�Ǵ����ı�������˵�����ɣ�
(2)����̽峣���̽�������ı���ABCD����Ա�AB��CD��BC��AD֮���������ϵ��
�������:��Ҫ������������������
д��֤�����̣��Ȼ���ͼ�Σ�д����֪����֤��
(3)����������ͼ3���ֱ���Rt��ACB��ֱ�DZ�AC��б��ABΪ��������������ACFG��������ABDE������CE��BG��GE����֪AC=4��AB=5,��GE����
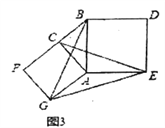
���𰸡���1���ı���ABCD�Ǵ����ı���,���ɼ�����;��2��������ۣ������ı��ε�����Աߵ�ƽ�������,���̼�����;��3��GE=![]()
�������������������1�����ݴ�ֱƽ���ߵ��ж������ɵã�ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ����۵�֤��
��2�����ݴ�ֱ�Ķ���ɵá�AED=��AEB=��BEC=��CED=90�����ɹ��ɶ�����AD2+BC2=AE2+DE2+BE2+CE2�������õ��𰸣�
��3������CG��BE������������GAB�ա�CAE����֪��ABG=��AEC�������õ��ı���BCGE�Ǵ����ı��Σ����������ݴ����ı��ε����ʡ����ɶ����Լ���2���Ľ��۽��м�����⣬������ɽ��.
���������
�⣺��1���ı���ABCD�Ǵ����ı��Σ�
֤������AB=AD��
���A���߶�BD�Ĵ�ֱƽ�����ϣ�
��CB=CD��
���C���߶�BD�Ĵ�ֱƽ�����ϣ�
��ֱ��AC���߶�BD�Ĵ�ֱƽ���ߣ�
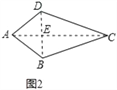
��AC��BD�����ı���ABCD�Ǵ����ı��Σ�
��2��������ۣ������ı��ε�����Աߵ�ƽ������ȣ�
��ͼ2����֪�ı���ABCD�У�AC��BD������ΪE��
��֤��AD2+BC2=AB2+CD2
֤������AC��BD��
���AED=��AEB=��BEC=��CED=90����
�ɹ��ɶ����ã�AD2+BC2=AE2+DE2+BE2+CE2��
AB2+CD2=AE2+BE2+CE2+DE2��
��AD2+BC2=AB2+CD2��
��3������CG��BE��
�ߡ�CAG=��BAE=90����
���CAG+��BAC=��BAE+��BAC������GAB=��CAE��
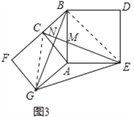
�ڡ�GAB�͡�CAE�У�
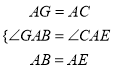 ��
��
���GAB�ա�CAE��
���ABG=��AEC���֡�AEC+��AME=90����
���ABG+��AME=90������CE��BG��
���ı���CGEB�Ǵ����ı��Σ�
�ɣ�2���ã�CG2+BE2=CB2+GE2��
��AC=4��AB=5��
��BC=3��CG=4![]() ��BE=5
��BE=5![]() ��
��
��GE2=CG2+BE2��CB2=73��
��GE=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У���ȷ������ ��
A. x3x3=x6 B. 3x2+2x3=5x5 C. ��x2��3=x5 D. ��ab��3=a3b
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������y=2x2����ƽ��3����λ��������ƽ��5����λ���õ��������ߵı���ʽΪ�� ��
A.y=2��x��3��2��5
B.y=2��x+3��2+5
C.y=2��x��3��2+5
D.y=2��x+3��2��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���Թ�˾���۲�Ϊ�˶����¸��µ����ۼƻ�����20λ����Ա���µ�������������ͳ��I���Ƴ���ͼ��ʾ��ͳ��ͼ������20λ������Ա������������ƽ��������λ���������ֱ���( )
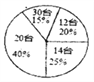
A. 19��20��14 B. 18.4��20��20 C. 19�� 20�� 20 D. 18.4��25��20
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�����κ�����ͼ�����ϣ���������Ϊ��2��3������ô������κ����Ľ���ʽ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬AC=6��BC=8�� 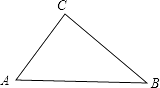
��1����ֱ�ߺ�Բ���ڱ�BC����һ��D��ʹD��AB�ľ������CD��
��2�����㣨1�����߶�CD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
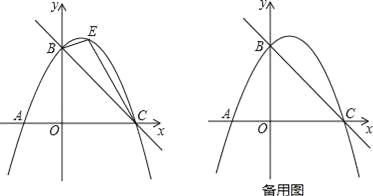
����Ŀ����ͼ��ֱ��y=��![]() x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+
x+3��x�ύ�ڵ�C����y�ύ�ڵ�B��������y=ax2+![]() x+c����B��C���㣮
x+c����B��C���㣮
��1���������ߵĽ���ʽ��
��2����ͼ����E��ֱ��BC�Ϸ��������ϵ�һ���㣬����BEC������ʱ���������E���������BEC��������ֵ��
��3���ڣ�2���Ľ����£�����E��y���ƽ���߽�ֱ��BC�ڵ�M������AM����Q�������߶Գ����ϵĶ��㣬�����������Ƿ���ڵ�P��ʹ����P��Q��A��MΪ������ı�����ƽ���ı��Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y��x2��x��1��x���һ������Ϊ(m��0)�������ʽm2��m��2014��ֵΪ_____��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com