
【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8. 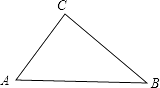
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上有A. B.C三点,分别代表24,10,10,两只电子蚂蚁甲、乙分别从A.C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
![]()
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A. B.C三点的距离和为40个单位?
(3)当甲到A. B.C三点的距离和为40个单位时,甲调头原速返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】彭山的枇杷大又甜,在今年5月18日“彭山枇杷节”期间,从山上5棵枇杷树上采摘到了200千克枇杷,请估计彭山近600棵枇杷树今年一共收获了枇杷千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
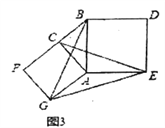
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在①ab是一次单项式;②单项式﹣x2y的系数是﹣1;③3+x2﹣4x是按x的降幂排列的;④数4是单项式;这四句话中不正确的是( )
A.①③
B.②③
C.②④
D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,命题p:“B≠60°“,命题q:“△ABC的三个内角A,B,C不成等差数列“,那么p是q的( )
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数 ![]() 的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
的图象与x轴与交于点A、点B(2,0),与y轴交于点C,∠ACB=90o.
(1)求二次函数解析式;
(2)直线![]() 与
与![]() 轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
轴平行,分别交线段AB、CB于点E、F,且与抛物线交于点P.
①求线段PF取得最大值时,OE的长;
②四边形ACPB的面积是否存在最大值?如果存在求出此最大值和点P的坐标;如果不存在,说明理由.
(3)不解方程组,直接写出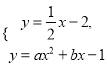 的解.
的解.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com