
【题目】已知数轴上有A. B.C三点,分别代表24,10,10,两只电子蚂蚁甲、乙分别从A.C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
![]()
(1)甲、乙多少秒后相遇?
(2)甲出发多少秒后,甲到A. B.C三点的距离和为40个单位?
(3)当甲到A. B.C三点的距离和为40个单位时,甲调头原速返回,当甲、乙在数轴上再次相遇时,相遇点表示的数是多少?
【答案】(1)甲、乙3.4秒后相遇;(2)甲出发2秒或5秒后,甲到A. B. C三点的距离和为40个单位;(3) 甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.
【解析】分析:(1)可设x秒后甲与乙相遇,根据相遇时甲与乙所行路程之和为34列出方程,求解即可;(2)设y秒后甲到A,B,C三点的距离之和为40个单位,分甲应为于AB或BC之间两种情况讨论即可求解;(3)设z秒后甲、乙在数轴上再次相遇,那么此时甲、乙表示在数轴上为同一点,依此列出方程求解即可.
本题解析:
(1)设xs后甲与乙相遇
4x+6x=34,
解得:x=3.4s,
4×3.4=13.6,-24+13.6=-10.4;
(2)设x秒后,甲到A,B,C的距离和为40个单位.
B点距A,C两点的距离为14+20=34<40,
A点距B、C两点的距离为14+34=48>40,
C点距A、B的距离为34+20=54>40,
故甲应位于AB或BC之间.
①AB之间时:4x+(14-4x)+(14-4x+20)=40,x=2s;
②BC之间时:4x+(4x-14)+(34-4x)=40,x=5s,
(3)设y秒后甲到A,B,C三点的距离之和为40个单位,
B点距A,C两点的距离为14+20=34<40,A点距B、C两点的距离为14+34=48>40,C点距A、B的距离为34+20=54>40,故甲应为于AB或BC之间.
①AB之间时:4y+(14-4y)+(14-4y+20)=40
解得y=2;
②BC之间时:4y+(4y-14)+(34-4y)=40,
解得y=5.
①甲从A向右运动2秒时返回,设y秒后与乙相遇.此时甲、乙表示在数轴上为同一点,所表示的数相同.
甲表示的数为:-24+4×2-4y;乙表示的数为:10-6×2-6y,
依据题意得:-24+4×2-4y=10-6×2-6y,
解得:y=7,
相遇点表示的数为:-24+4×2-4y=-44(或:10-6×2-6y=-44),
②甲从A向右运动5秒时返回,设y秒后与乙相遇.
甲表示的数为:-24+4×5-4y;乙表示的数为:10-6×5-6y,
依据题意得:-24+4×5-4y=10-6×5-6y,
解得:y=-8(不合题意舍去),
即甲从A向右运动2秒时返回,能在数轴上与乙相遇,相遇点表示的数为-44.


科目:初中数学 来源: 题型:
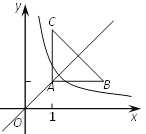
【题目】如图,Rt△ABC在第一象限, ![]() ,AB=AC=2,点A在直线
,AB=AC=2,点A在直线![]() 上,其中点A的横坐标为1,且AB∥
上,其中点A的横坐标为1,且AB∥![]() 轴,AC∥
轴,AC∥![]() 轴,若双曲线
轴,若双曲线![]() 与
与![]() 有交点,则k的取值范围是_______.
有交点,则k的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图. 根据以上信息,解答下列问题: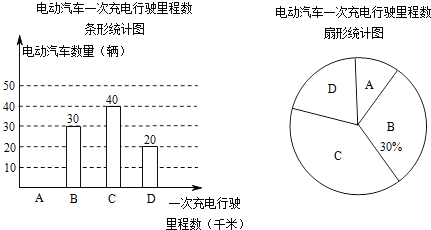
(1)问这次被抽检的电动汽车共有几辆?
(2)补全条形统计图,并求出C等级对应的圆心角度数.
(3)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知, A、B、C、D、E是反比例函数![]() (x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)。
(x>0)图象上五个整数点(横、纵坐标均为整数),分别以这些点向横轴或纵轴作垂线段,由垂线段所在的正方形边长为半径作四分之一圆周的两条弧,组成如图5所示的五个橄榄形(阴影部分),则这五个橄榄形的面积总和是 (用含π的代数式表示)。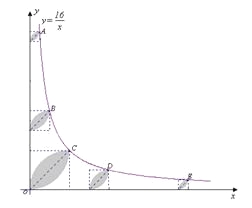
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同.小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点Q的坐标(x,y).
(1)画树状图或列表,写出点Q所有可能的坐标;
(2)求点Q(x,y)在函数y=-x+5的图象上的概率;
(3)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6则小明胜,若x、y满足xy<6则小红胜,这个游戏公平吗?说明理由;若不公平,请写出公平的游戏规则.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,AC=6,BC=8. 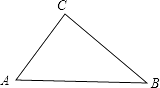
(1)用直尺和圆规在边BC上找一点D,使D到AB的距离等于CD.
(2)计算(1)中线段CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com