
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
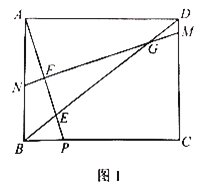
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
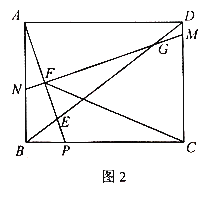
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由等角对等边可得![]() ,再由对顶角相等推出
,再由对顶角相等推出![]() ,然后利用等角的余角相等即可得证;
,然后利用等角的余角相等即可得证;
(2)在![]() 中,利用勾股定理可求出BD=10,然后由等角对等边得到
中,利用勾股定理可求出BD=10,然后由等角对等边得到![]() ,进而求出BP=2,再利用
,进而求出BP=2,再利用![]() 推出
推出![]() ,由垂直平分线推出
,由垂直平分线推出![]() ,即可得到
,即可得到![]() 的值;
的值;
(3)连接CG,先由勾股定理求出![]() ,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出
,由(2)的条件可推出BE=DG,再证明△ABE≌△CDG,从而求出![]() ,并推出
,并推出![]() ,最后在
,最后在![]() 中,即可求出
中,即可求出![]() 的值.
的值.
(1)证明:![]() ,
,
![]()
![]()
![]()
∵MN⊥AP
∴∠GFE=90°
∴∠BGN+∠GEF=90°
又![]()
![]()
![]()
(2)在矩形ABCD中,![]()
∴在![]() 中,
中,![]()
![]()
又∵在矩形ABCD中,![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴![]()
![]()
![]()
∵MN垂直平分AP
![]()
(3)如图,连接CG,
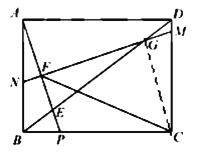
在![]() 中,
中,![]()
![]()
![]()
在![]() 中,
中,![]()
![]()
![]()
![]()
又∵在矩形ABCD中,![]()
![]()
在△ABE和△CDG中,
∵AB=DC,∠ABE=∠CDG,BE=DG
![]()
![]()
![]()
![]()
![]()
∴在![]() 中,
中,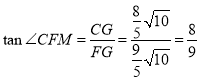


科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
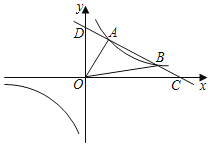
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校3月份开展网络授课教学,该校随机抽取部分学生,按四个类别(A、很喜欢;B、喜欢;C、一般;D、不喜欢;)统计它们对网络授课的接受情况,并将结果绘制成如下两幅不完整的统计图:
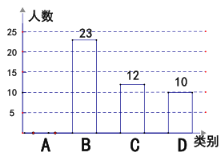
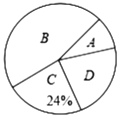
(1)这次共抽取_________名学生进行统计调查;扇形统计图中,D类所对应的扇形圆心角的大小为_______;
(2)将条形图补充完整;
(3)该校共有1500名学生,估计该校表示“喜欢”网络授课的B类的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】上海世博会已于2010年4月30日开幕,各国游客都被吸引到了这个地方,据统计到5月10号为止最高单日接待量已达到100万人次,其中中国馆自然是最受欢迎的展馆,在世博会开园第一天共接待了游客3万余人,而外国场馆中最受欢迎的依次是瑞士馆、法国馆、德国馆、西班牙馆、日本馆.现将某天世博会最受欢迎的6个馆的参观人数用统计图①②分别表示如下:
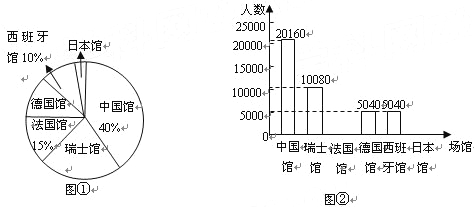
请根据统计图回答下列问题:
(1)这一天参观这6个场馆的总人数为 __ ,其中参观日本馆的人数有__,德国馆所在扇形的圆心角度数为__;
(2)请将条形统计图补充完整;
(3)小宝和小贝都想利用暑假去上海参观世博会,恰好张伯伯有一张世博会的门票,小宝和小贝都想得到这张门票.于是他们决定用转转盘的游戏来决定这张票由谁获得,游戏规则如下:将一质地均匀的转盘等分成5个面积相等的扇形,上面分别标有数字 -l,4,5,-6,0,小宝和小贝均随机地转转盘一次,把指针指向区域内的数字分别记为x、y.若指针指在边界,则重新转一次直到指针指向一个区域内为止,然后他们计算出xy的值.规定:当xy的值为负数时,门票归小宝;xy的值为正数时,门票归小贝.请利用表格或树状图游戏对双方公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为5元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为6元/
的价格为6元/![]() ,超过
,超过![]() 部分的价格为4元/
部分的价格为4元/![]() .设小张在同一个批发店一次购买苹果的数量为
.设小张在同一个批发店一次购买苹果的数量为![]() .
.
(1)根据题意填表:
一次购买数量/ | 20 | 50 | 150 | … |
甲批发店花费/元 | 250 | … | ||
乙批发店花费/元 | 350 | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若小张在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小张在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的___________批发店购买花费少;
,则他在甲、乙两个批发店中的___________批发店购买花费少;
③若小张在同一个批发店一次购买苹果花费了460元,则他在甲、乙两个批发店中的___________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装加工厂甲、乙两个车间共同加工一款休闲装,且每人每天加工的件数相同,甲车间比乙车间少10人,甲车间每天加工服装400件,乙车间每天加工服装600件.
(1)求甲、乙两车间各有多少人;
(2)甲车间更新了设备,平均每人每天加工的件数比原来多了10件,乙车间的加工效率不变,在两个车间总人数不变的情况下,加工厂计划从乙车间调出一部分人到甲车间,使每天两个车间加工的总数不少于1314件,求至少要从乙车间调出多少人到甲车间.
查看答案和解析>>
科目:初中数学 来源: 题型:
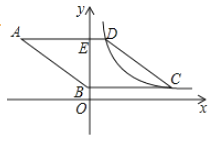
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE
(1)求出k值.
(2)求出△OCD的面积
(3)试探究坐标轴上是否存在点P,使得△PCD的面积等于菱形ABCD的面积的一半,如果存在,请直接写出点P的坐标;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() 为射线
为射线![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() .
.
(1)如图1,若![]() 点与点
点与点![]() 重合,且
重合,且![]() ,求
,求![]() 的长;
的长;
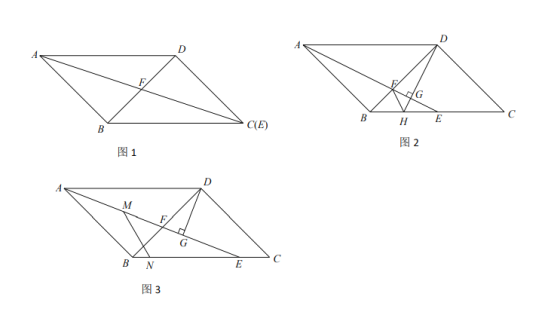
(2)如图2,当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 于
于![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .求证:
.求证:![]() .
.
(3)如图3,当点![]() 在射线
在射线![]() 上运动时,过点
上运动时,过点![]() 作
作![]() 于
于![]() 为
为![]() 的中点,点
的中点,点![]() 在
在![]() 边上且
边上且![]() ,已知
,已知![]() ,请直接写出
,请直接写出![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com