
【题目】如图,将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE,DE的延长线恰好经过AC的中点F,连接AD,CE.
(1)求证:AE=CE;
(2)若BC=![]() ,求AB的长.
,求AB的长.

科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有A,B两个转盘,其中转盘A被分成4等份,转盘B被分成3等份,并在每一份内标上数字.现甲、乙两人同时各转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)计算点P在函数y= ![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )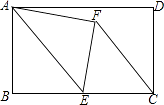
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+”是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(1)求点A(![]() ,
, ![]() )的勾股值[A],
)的勾股值[A],
(2)若将点A向上平移3个单位,再向左平移2个单位后得到点B,请直接写出点B的坐标,并求出点B的勾股值 [B];
(3)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com