【题目】二次函数y=x2﹣x+m（m为常数）的图象如图所示，当x=a时，y＜0；那么当x=a﹣1时，函数值（ ）
A.y＜0
B.0＜y＜m
C.y＞m
D.y=m
寒假学与练系列答案科目：初中数学 来源： 题型：
【题目】学校准备购进一批篮球和足球，买1个篮球和2个足球共需170元，买2个篮球和1个足球共需190元．
（1）求一个篮球和一个足球的售价各是多少元？
（2）学校欲购进篮球和足球共100个，且足球数量不多于篮球数量的2倍，求出最多购买足球多少个？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】按要求完成下列推理证明．
如图，已知点D为BC延长线上一点，CE∥AB．
求证：∠A+∠B+∠ACB＝180°
证明：∵CE∥AB，
∴∠1＝ ，（ ）
∠2＝ ，（ ）
又∠1+∠2+∠ACB＝180°（平角的定义），
∴∠A+∠B+∠ACB＝180°
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】汽车租赁公司拥有某种型号的汽车100辆．公司在经营中发现每辆车的月租金x（元）与每月租出的车辆数（y）有如下关系：
x（元） | 3000 | 3200 | 3500 | 4000 |
y（辆） | 100 | 96 | 90 | 80 |
（1）观察表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求按照表格呈现的规律，每月租出的车辆数y（辆）与每辆车的月租金x（元）之间的关系式．
（2）已知租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元．用含x（x≥3000）的代数式填表：
租出的车辆数（辆） | 未租出的车辆数（辆） | ||
租出每辆车的月收益（元） | 所有未租出的车辆每月的维护费（元） |
（3）若你是该公司的经理，你会将每辆车的月租金定为多少元，才能使公司获得最大月收益？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线y＝
x﹣2与x轴交于点A，以OA为斜边在x轴上方作等腰直角三角形OAB，将△OAB沿x轴向右平移，当点B落在直线y＝x﹣2上时，则△OAB平移的距离是_____．
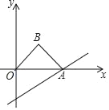
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴上点
表示的数为6，点
位于点的左侧，
，动点
从点出发，以每秒3个单位长度的速度沿数轴向左运动，动点
从点出发，以每秒2个单位长度的速度沿数轴向右运动．
（1）点表示的数是多少？
（2）若点，同时出发，求：
①当点与相遇时，它们运动了多少秒？相遇点对应的数是多少？
②当
个单位长度时，它们运动了多少秒？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC，D是边BC上一点，DE⊥AB，DF⊥AC，垂足分别是E,F，△AEF∽△ABC．
（1）求证：△AED≌△AFD；
（2）若BC=2AD，求证：四边形AEDF是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE，DE的延长线恰好经过AC的中点F，连接AD，CE．
（1）求证：AE＝CE；
（2）若BC＝
，求AB的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
