
【题目】如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E,F,△AEF∽△ABC.
(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形.
【答案】
(1)证明:∵△AEF∽△ABC,
∴ ![]() =
= ![]() ,
,
∵AB=AC,
∴AE=AF,
∵DE⊥AB,DF⊥AC,
∴∠AED=∠AFD=90°,
在Rt△AED和Rt△AFD中,
![]() ,
,
∴Rt△AED≌Rt△AFD
(2)证明:∵Rt△AED≌Rt△AFD,
∴∠EAD=∠FAD,
∵AB=AC,
∴AD⊥BC,BC=2BD,
∵BC=2AD,
∴BD=AD,
∵AD⊥BC,
∴∠ADB=90°,
∴∠B=∠BAD=45°,
∴∠BAC=2∠BAD=90°,
∵∠AED=∠AFD=90°,
∴四边形AEDF是矩形,
∵AE=AF,
∴矩形AEDF是正方形
【解析】(1)由相似三角形得性质得AE=AF,然后由HL定理判断出Rt△AED≌Rt△AFD;(2)由Rt△AED≌Rt△AFD得∠EAD=∠FAD,再由等腰三角形的三线合一得AD⊥BC,BC=2BD,由BC=2AD,得出∠B=∠BAD=45°,从而判断四边形AEDF是矩形,最后由一组邻边相等的矩形是正方形得出答案。
【考点精析】通过灵活运用正方形的判定方法和相似三角形的性质,掌握先判定一个四边形是矩形,再判定出有一组邻边相等;先判定一个四边形是菱形,再判定出有一个角是直角;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=x2﹣x+m(m为常数)的图象如图所示,当x=a时,y<0;那么当x=a﹣1时,函数值( )
A.y<0
B.0<y<m
C.y>m
D.y=m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南通某校为了了解家长和学生参与南通安全教育平台“![]() 防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下
防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下![]() 类情形:
类情形:
A.仅学生自己参与;
B.家长和学生一起参与;
C.仅家长参与;
D.家长和学生都未参与
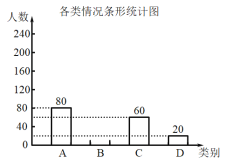
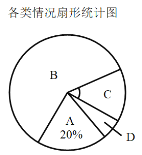
请根据上图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生?
(2)补全条形统计图,并在扇形统计图中计算![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将30°、45°、60°的三角函数值填入表中,则从表中任意取一个值,是 ![]() 的概率为( )
的概率为( )
α | 30° | 45° | 60° |
sinα | |||
cosα | |||
tanα |
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+”是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(1)求点A(![]() ,
, ![]() )的勾股值[A],
)的勾股值[A],
(2)若将点A向上平移3个单位,再向左平移2个单位后得到点B,请直接写出点B的坐标,并求出点B的勾股值 [B];
(3)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com