
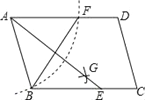
【题目】如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG交BC于点E.若BF=6,AB=5,则AE的长为____.
【答案】8
【解析】
由基本作图得到AB=AF,加上AO平分∠BAD,则根据等腰三角形的性质得到AO⊥BF,BO=FO=![]() BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
BF=3,再根据平行四边形的性质得AF∥BE,所以∠1=∠3,于是得到∠2=∠3,根据等腰三角形的判定得AB=EB,然后再根据等腰三角形的性质得到AO=OE,最后利用勾股定理计算出AO,从而得到AE的长.
解:连结EF,AE与BF交于点O,如图,
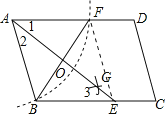
∵AB=AF,AO平分∠BAD,
∴AO⊥BF,BO=FO=![]() BF=3,
BF=3,
∵四边形ABCD为平行四边形,
∴AF∥BE,
∴∠1=∠3,
∴∠2=∠3,
∴AB=EB,
而BO⊥AE,
∴AO=OE,
在Rt△AOB中,AO=![]() =4,
=4,
∴AE=2AO=8.
故答案为:8.


科目:初中数学 来源: 题型:
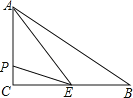
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以1cm/s的速度沿A→C运动,然后以2cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=__时,△APE的面积等于6 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.
(1)求一个篮球和一个足球的售价各是多少元?
(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
求1+2+22+23+24+…+22020的值.
解:设S=1+2+22+23+24+…+22020,将等式两边同时乘以2得,
2S=2+22+23+24+25+…+22021.
将下式减去上式,得2S﹣S=22021﹣1,即S=22021﹣1.
即1+2+22+23+24+…+22020=22021﹣1
仿照此法计算:
(1)1+3+32+33+…+320;
(2)![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中有3个红球,3个绿球和若干个白球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.
(1)若袋子内白球有4个,任意摸出一个球是绿球的概率是多少?
(2)如果任意摸出一个球是绿球的概率是![]() ,求袋子内有几个白球?
,求袋子内有几个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.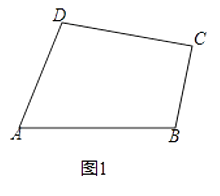
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.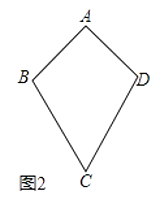
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.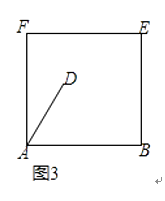
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x(元) | 3000 | 3200 | 3500 | 4000 |
y(辆) | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识,求按照表格呈现的规律,每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数(辆) | 未租出的车辆数(辆) | ||
租出每辆车的月收益(元) | 所有未租出的车辆每月的维护费(元) |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是边BC上一点,DE⊥AB,DF⊥AC,垂足分别是E,F,△AEF∽△ABC.
(1)求证:△AED≌△AFD;
(2)若BC=2AD,求证:四边形AEDF是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com