【题目】类比特殊四边形的学习，我们可以定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．
（1）【探索体验】如图1，已知在四边形ABCD中，∠A=40°，∠B=100°，∠C=120°．求证：四边形ABCD是“等对角四边形”．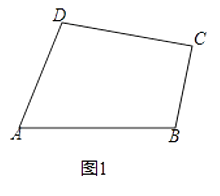

（2）如图2，若AB=AD=a，CB=CD=b，且a≠b，那么四边形ABCD是“等对角四边形”吗？试说明理由．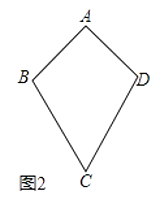

（3）【尝试应用】如图3，在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD，若已经确定DA=4m，∠DAB=60°，是否在正方形ABEF内（包括边上）存在一点C，使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大？若存在，试求出四边形ABCD的最大面积；若不存在，请说明理由．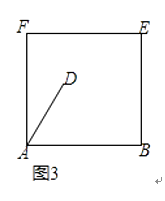

参考答案：

【答案】
（1）证明：∵在四边形ABCD中，∠A=40°，∠B=100°，∠C=120°．

∴∠D=360°﹣∠A﹣∠B﹣∠C=100°，∠A≠∠C，

∴∠D=∠D，

∴四边形ABCD是“等对角四边形”


（2）证明：如图2，连接BD，

∵AB=AD，CB=CD，

∴∠ABD=∠ADB，∠CBD=∠CDB，

∴∠ABD+∠CBD=∠ADB+∠CDB，

∴∠ABC=∠ADC，

∵AB=AD=a，CB=CD=b，且a≠b，且BD=BD，

∴△ABD与△CBD不相似，

∴∠A≠∠C，

∴四边形ABCD是“等对角四边形”


（3）如图3，连接BD，

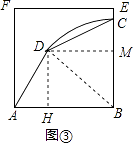
当∠DAB=∠BCD=60°时，四边形ABCD是“等对角四边形”，

此时点C在BD为弦的 上，

要使四边形ABCD的面积最大，则点C在边BE上，

过点D作DH⊥AB于点H，作DM⊥BC于点M，

在Rt△ADH中，∠DAH=60°，AD=4，

∴AH=2，DH=2 ，

∴BH=AB﹣AH=4，

∵四边形DHBM是矩形，

∴BM=DH=2 ，DM=BH=4，

在Rt△DMC中，∠DCM=60°，

∴CM= DM= ，

∴BC=BM+CM=2 + = ，

∴S四边形ABCD=S△ABD+S△BCD= ×6×2 + × ×4= （m2）


【解析】（1）求出第4个角度数，按照定义即可判断出结论；（2）利用等边对等角定理，须连接BD，得出有一组对角相等，再证另一组对角不等，得出结论;（3）借鉴（2）的方法，要使∠BCD=60°，C需在以BD为弦的弧BD上，若四边形ABCD的面积最大，则点C在边BE上，才能使高最大，进而面积最大.
【考点精析】掌握三角形的面积和圆周角定理是解答本题的根本，需要知道三角形的面积=1/2×底×高；顶点在圆心上的角叫做圆心角;顶点在圆周上，且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半．

关闭