
����Ŀ�����������
![]() ��
��![]() �ֱ���ʲô��ʱ������ʽ
�ֱ���ʲô��ʱ������ʽ![]() ��
��![]() ��ȣ�
��ȣ�
�Ķ����⣺
��ν���ʽ������ָ�������κ���ֵ������ʽ�еı������������ߵ�ֵ����ȵĵ�ʽ�������÷��š�![]() ������ʾ��ȣ�����������ڡ������ǣ����������Ҳ���Ա���Ϊ����֪
������ʾ��ȣ�����������ڡ������ǣ����������Ҳ���Ա���Ϊ����֪![]() �������ϵ��
�������ϵ��![]() ��
��![]() ��
��
��������
������1����ֵ���뷨���ɺ��ʽ�ĸ������ÿ��һ����ֵ�����������е�![]() �����ɵõ�һ������
�����ɵõ�һ������![]() ��
��![]() �ķ��̣���ˣ�Ҫ���
�ķ��̣���ˣ�Ҫ���![]() ��
��![]() ��ֵ��ֻ��Ҫ��������ͬ����ֵ�ֱ����ʽ�е�
��ֵ��ֻ��Ҫ��������ͬ����ֵ�ֱ����ʽ�е�![]() ���Ϳ��Եõ�һ������
���Ϳ��Եõ�һ������![]() ��
��![]() �Ķ�Ԫһ�η����飬����������飬�������
�Ķ�Ԫһ�η����飬����������飬�������![]() ��
��![]() ��
��
�⣺�ֱ���![]() ��
��![]() ����ʽ�е�
����ʽ�е�![]() ����
����
![]()
��֮����![]()
������2��ϵ���ȽϷ���
���� ���![]() ��
��
��ô![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�������������Ҳ���������⣺
�⣺������![]() ��
��
�Ƚ϶�Ӧ���ϵ������![]() ��
��![]() ��
��
��ش���������⣺
��1����֪����ʽ![]() ����
����![]() ��
��![]() ��ֵ��
��ֵ��
��2�����![]() ��
��![]() ������
������![]() ����
����![]() ��ֵ����ʽ��
��ֵ����ʽ��
���𰸡���1��m=-1��n=2����2��![]() ����ʽΪ
����ʽΪ![]() ��
��
��������
��1���Զ���ʽ�ұ����ö���ʽ�˶���ʽ�ķ���չ�����Ƚ϶�Ӧ���ϵ�����õ������飬��֮���ɣ�
��1���ȸ��������֪��ʽ��һ����ϵ��Ϊ1���ʿ�����ʽΪ![]() ���ٸ������⣬�Ƚ϶�Ӧ���ϵ�����г����̼������
���ٸ������⣬�Ƚ϶�Ӧ���ϵ�����г����̼������![]() ��
��![]() ��ֵ��
��ֵ��
��1��![]()
![]() ��
��
�Ƚ϶�Ӧ���ϵ������ ��
��
��֮����![]() ��
��
��2����Ϊ![]() ��������ʽ����ߴ���Ϊһ�Σ�����ϵ��Ϊ
��������ʽ����ߴ���Ϊһ�Σ�����ϵ��Ϊ![]() ��
��
������ʽΪ![]() �������⣬�ã�
�������⣬�ã�
![]()
![]() ��
��
�Ƚ϶�Ӧ���ϵ������![]() ��
��
��֮����
![]() ����ʽΪ
����ʽΪ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���A��60������E��F�ֱ�ΪAD��DC�ϵĶ��㣬��EBF=60������E�ӵ�A���D�˶��Ĺ����У�AE��CF�ij��ȣ� ��

A. ������ B. ��С
C. ���ֲ�������EF�ij������ D. ���ֲ�������AB�ij������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABCD�У��Խ���AC��BD�ཻ�ڵ�O�����AC=12��BD=10��AB=m����ôm��ȡֵ��Χ�ǣ�������
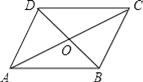
A. 1��m��11 B. 2��m��22 C. 10��m��12 D. 5��m��6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ������C��AB���ӳ����ϣ�CD���O�����ڵ�D��CE��AD����AD���ӳ����ڵ�E��
��1����֤����BDC=��A��
��2����CE=2��DE=1����AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ı��ε�ѧϰ�����ǿ��Զ��壺��һ��Խ���ȶ���һ��ԽDz���ȵ��ı��ν������ȶԽ��ı��Ρ���
��1����̽�����顿��ͼ1����֪���ı���ABCD�У���A=40�㣬��B=100�㣬��C=120�㣮��֤���ı���ABCD�ǡ��ȶԽ��ı��Ρ���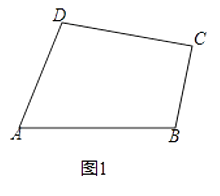
��2����ͼ2����AB=AD=a��CB=CD=b����a��b����ô�ı���ABCD�ǡ��ȶԽ��ı��Ρ�����˵�����ɣ�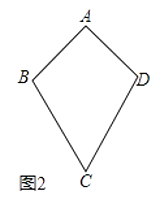
��3��������Ӧ�á���ͼ3���ڱ߳�Ϊ6��������ľ��ABEF�ϲó����ȶԽ��ı��Ρ�ABCD�����Ѿ�ȷ��DA=4m����DAB=60�㣬�Ƿ���������ABEF�ڣ��������ϣ�����һ��C��ʹ�ı���ABCD�ԡ�DAB=��BCDΪ�ȶԽǵ��ı��ε������������ڣ�������ı���ABCD�����������������ڣ���˵�����ɣ�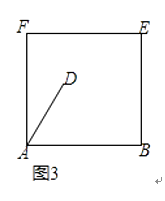
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�ACΪ�Խ��ߣ�EΪAB��һ�㣬����E��EF��AD����AC,DC�ֱ��ڵ�G��F��HΪCG���е㣬����DE��EH��DH��FH�����н����н�����ȷ���У� ��
��EG=DF��
�ڡ�AEH+��ADH=180�㣻
�ۡ�EHF�ա�DHC��
���� ![]() =
= ![]() ����S��EDH=13S��CFH ��
����S��EDH=13S��CFH �� 
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�Ϊ�������˿ͣ������˿�������ת����ת�̣���ͼ��ת�̱����ȷ�Ϊ20�ݣ������涨���˿�ÿ����200Ԫ����Ʒ�����ܻ��һ��ת��ת�̵Ļ��ᣮ���ת��ֹͣ��ָ�����ö���ɫ����ɫ����ɫ������ô�˿;Ϳ��Էֱ���200Ԫ��100Ԫ��50Ԫ�Ĺ���ȯ��ƾ����ȯ�����ڸ��̳������������˿Ͳ�Ը��תת�̣���ô����ֱ�ӻ�ù���ȯ30Ԫ��
��1����ת��һ��ת�̻�ù���ȯ�ĸ��ʣ�
��2��תת�̺�ֱ�ӻ�ù���ȯ������Ϊ���ַ�ʽ�Թ˿����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ٽ���ij�̳�������չ���ж������������˿͡��Ĵ�������Բ��ֽ��մ�������д������ۣ�����![]() ����մ������
����մ������![]() ��
��![]() ����մ������
����մ������![]() �ۣ���֪����ǰ������
�ۣ���֪����ǰ������![]() ��
��![]() ����մ������
����մ������![]() ��
��![]() ����մ������Ҫ
����մ������Ҫ![]() Ԫ�����ۺ���
Ԫ�����ۺ���![]() ��
��![]() ����մ������
����մ������![]() ��
��![]() ����մ������Ҫ
����մ������Ҫ![]() Ԫ��
Ԫ��
![]() ����ۺ�
����ۺ�![]() ������մ����ÿ�зֱ�Ϊ����Ԫ��
������մ����ÿ�зֱ�Ϊ����Ԫ��
![]() �����ڼ䣬ij��˾�ƻ�ΪԱ���ɹ�
�����ڼ䣬ij��˾�ƻ�ΪԱ���ɹ�![]() �н��մ�������ܷ��ò�����
�н��մ�������ܷ��ò�����![]() Ԫ���������Թ���
Ԫ���������Թ���![]() ����մ�������ٺУ�
����մ�������ٺУ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
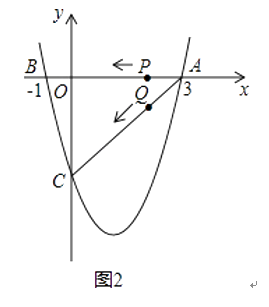
����Ŀ����ͼ1��ע����ͼ2��ȫ��ͬ�������κ���y= ![]() x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
x2+bx+c��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��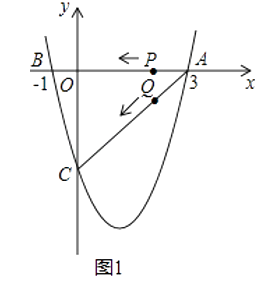
��1����ö��κ����Ľ���ʽ��
��2����������ߵĶ���ΪD�����ACD�����������ͼ1��̽������
��3������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����P��Q�˶���t��ʱ����APQ��PQ���ڵ�ֱ�߷��ۣ���Aǡ��������������E�㴦����ֱ���ж���ʱ�ı���APEQ����״�������E�����꣨����ͼ2��̽������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com