
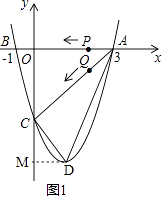
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.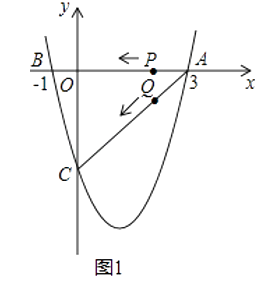
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
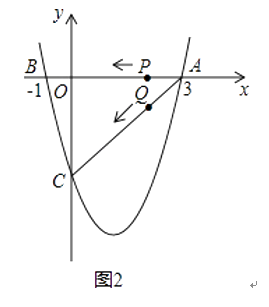
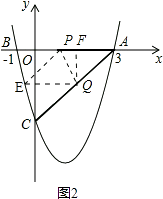
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
【答案】
(1)解:∵二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0),
∴ 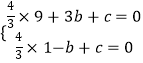 ,
,
解得: 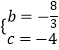 ,
,
∴y= ![]() x2﹣
x2﹣ ![]() x﹣4
x﹣4
(2)解:过点D作DM⊥y轴于点M,
∵y= ![]() x2﹣
x2﹣ ![]() x﹣4=
x﹣4= ![]() (x﹣1)2﹣
(x﹣1)2﹣ ![]() ,
,
∴点D(1,﹣ ![]() )、点C(0,﹣4),
)、点C(0,﹣4),
则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC
= ![]() ×(1+3)×
×(1+3)× ![]() ﹣
﹣ ![]() ×(
×( ![]() ﹣4)×1﹣
﹣4)×1﹣ ![]() ×3×4
×3×4
=4
(3)解:四边形APEQ为菱形,E点坐标为(﹣ ![]() ,﹣
,﹣ ![]() ).理由如下
).理由如下
如图2,E点关于PQ与A点对称,过点Q作,QF⊥AP于F,
∵AP=AQ=t,AP=EP,AQ=EQ
∴AP=AQ=QE=EP,
∴四边形AQEP为菱形,
∵FQ∥OC,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]()
∴AF= ![]() t,FQ=
t,FQ= ![]() t
t
∴Q(3﹣ ![]() t,﹣
t,﹣ ![]() t),
t),
∵EQ=AP=t,
∴E(3﹣ ![]() t﹣t,﹣
t﹣t,﹣ ![]() t),
t),
∵E在二次函数y= ![]() x2﹣
x2﹣ ![]() x﹣4上,
x﹣4上,
∴﹣ ![]() t=
t= ![]() (3﹣
(3﹣ ![]() t)2﹣
t)2﹣ ![]() (3﹣
(3﹣ ![]() t)﹣4,
t)﹣4,
∴t= ![]() ,或t=0(与A重合,舍去),
,或t=0(与A重合,舍去),
∴E(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)将A、B两点的坐标代入函数y= ![]() x2+bx+c中,求得b、c进而求得解析式;(2)由解析式先求得D、C两点坐标,再根据则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式计算即可;(3)注意到P、Q运动速度相同,则△APQ运动时都为等腰三角形,由因A、E对称,则AP=EP,AQ=EQ,易得四边形AQEP为菱形,利用菱形对边平行且相等得性质可用t表示E点坐标,又E在二次函数的图像上,所以代入即可求t,进而E可表示。
x2+bx+c中,求得b、c进而求得解析式;(2)由解析式先求得D、C两点坐标,再根据则S△ACD=S梯形AOMD﹣S△CDM﹣S△AOC,列式计算即可;(3)注意到P、Q运动速度相同,则△APQ运动时都为等腰三角形,由因A、E对称,则AP=EP,AQ=EQ,易得四边形AQEP为菱形,利用菱形对边平行且相等得性质可用t表示E点坐标,又E在二次函数的图像上,所以代入即可求t,进而E可表示。


科目:初中数学 来源: 题型:
【题目】问题提出:
![]() ,
,![]() 分别是什么数时,多项式
分别是什么数时,多项式![]() 和
和![]() 恒等?
恒等?
阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“![]() ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知![]() ,求待定系数
,求待定系数![]() ,
,![]() .
.
问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的![]() ,即可得到一个关于
,即可得到一个关于![]() 与
与![]() 的方程.因此,要求出
的方程.因此,要求出![]() 与
与![]() 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的![]() ,就可以得到一个关于
,就可以得到一个关于![]() 与
与![]() 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得![]() 与
与![]() .
.
解:分别用![]() ,
,![]() 代替式中的
代替式中的![]() ,得
,得
![]()
解之,得![]()
(方法2—系数比较法)
定理 如果![]() ,
,
那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据这个定理,也可以这样解:
解:由题设![]() ,
,
比较对应项的系数,得![]() ,
,![]() .
.
请回答下面的问题:
(1)已知多项式![]() .求
.求![]() 与
与![]() 的值;
的值;
(2)如果![]() 被
被![]() 除后余
除后余![]() ,求
,求![]() 的值及商式.
的值及商式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在图中利用网格点和三角板画图或计算:
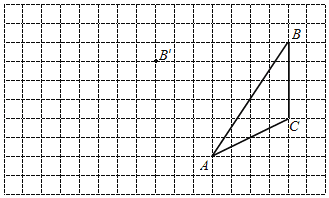
(1)在给定方格纸中画出![]() 平移后的
平移后的![]() (点
(点![]() 的对应点是点
的对应点是点![]() );
);
(2)画出![]() 边上的中线
边上的中线![]() ;
;
(3)画出![]() 边上的高线
边上的高线![]() ;
;
(4)记网格的边长为1,则在平移的过程中线段![]() 扫过区域的面积为
扫过区域的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( )
A.10
B.16
C.18
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A(﹣2,m),B
的图象交于A(﹣2,m),B
(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
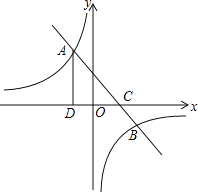
(1)求这两个函数的解析式:
(2)求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.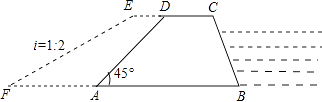
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com