
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 ![]() =
= ![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH . 
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF﹣GF,DF=CD﹣FC,
∴EG=DF,
故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH= ![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
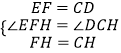 ,
,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF﹣∠HDC=∠AEF+∠ADF=180°,
故②正确;
③由②知:△EHF≌△DHC,
故③正确;
④∵ ![]() =
= ![]() ,
,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
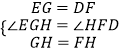 ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
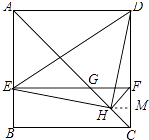
设HM=x,则CF=2x,
∴DF=2FC=4x,
∴DM=5x,DH= ![]() x,CD=6x,
x,CD=6x,
则S△CFH= ![]() ×HM×CF=
×HM×CF= ![]() x2x=x2,S△EDH=
x2x=x2,S△EDH= ![]() ×DH2=
×DH2= ![]() ×
× ![]() =13x2,
=13x2,
∴则S△EDH=13S△CFH,故④正确;
其中结论正确的有:①②③④,4个;
故D符合题意.
所以答案是:D.
【考点精析】本题主要考查了正方形的性质和相似三角形的判定与性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五名同学在一次数学测验中的平均成绩是80分,而
五名同学在一次数学测验中的平均成绩是80分,而![]() ,
,![]() ,
,![]() 三人的平均成绩是78分,下列说法一定正确的是( )
三人的平均成绩是78分,下列说法一定正确的是( )
A.![]() ,
,![]() 两人的平均成绩是83分B.
两人的平均成绩是83分B.![]() ,
,![]() 的成绩比其他三人都好
的成绩比其他三人都好
C.五人成绩的中位数一定是80分D.五人的成绩的众数一定是80分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
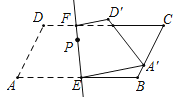
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
![]() ,
,![]() 分别是什么数时,多项式
分别是什么数时,多项式![]() 和
和![]() 恒等?
恒等?
阅读理解:
所谓恒等式,就是指不论用任何数值来代替式中的变量,左、右两边的值都相等的等式.我们用符号“![]() ”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知
”来表示恒等,读作“恒等于”.于是,上面的问题也可以表述为:已知![]() ,求待定系数
,求待定系数![]() ,
,![]() .
.
问题解决:
(方法1—数值代入法)由恒等式的概念,我们每用一个数值来代替问题中的![]() ,即可得到一个关于
,即可得到一个关于![]() 与
与![]() 的方程.因此,要求出
的方程.因此,要求出![]() 与
与![]() 的值,只需要用两个不同的数值分别代替式中的
的值,只需要用两个不同的数值分别代替式中的![]() ,就可以得到一个关于
,就可以得到一个关于![]() 与
与![]() 的二元一次方程组,解这个方程组,即可求得
的二元一次方程组,解这个方程组,即可求得![]() 与
与![]() .
.
解:分别用![]() ,
,![]() 代替式中的
代替式中的![]() ,得
,得
![]()
解之,得![]()
(方法2—系数比较法)
定理 如果![]() ,
,
那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据这个定理,也可以这样解:
解:由题设![]() ,
,
比较对应项的系数,得![]() ,
,![]() .
.
请回答下面的问题:
(1)已知多项式![]() .求
.求![]() 与
与![]() 的值;
的值;
(2)如果![]() 被
被![]() 除后余
除后余![]() ,求
,求![]() 的值及商式.
的值及商式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生汉字书写的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试方法是:听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50≤x<100,将其按分数段分为五组,绘制出以下不完整表格:
组别 | 成绩x(分) | 频数(人数) | 频率 |
一 | 50≤x<60 | 2 | 0.04 |
二 | 60≤x<70 | 10 | 0.2 |
三 | 70≤x<80 | 14 | b |
四 | 80≤x<90 | a | 0.32 |
五 | 90≤x<100 | 8 | 0.16 |
请根据表格提供的信息,解答以下问题:
(1)直接写出表中a= , b=;
(2)请补全右面相应的频数分布直方图;
(3)若决赛成绩不低于80分为优秀,则本次大赛的优秀率为 .
(4)请根据得到的统计数据,简要分析这些同学的汉字书写能力,并为提高同学们的书写汉字能力提一条建议(所提建议不超过20字)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD,延长AD到E,使DE=AD,连接BE与DC交于O点.
(1)求证:△BOC≌△EOD;
(2)当△ABE满足什么条件时,四边形BCED是菱形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于![]() 的二次函数
的二次函数![]() 和
和![]() ,若
,若![]() 与
与![]() 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数![]() 的表达式,并求出当
的表达式,并求出当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( )
A.10
B.16
C.18
D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com