
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
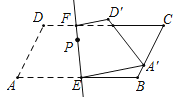
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
【答案】D
【解析】
连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.因为A、A′关于直线EF对称,推出P′A′=P′A,推出P′A′+P′C=P′A+P′C=AC,推出当点P与P′重合时,PA′+PC的值最小,最小值=AC的长;
如图,连接AC交EF于P′,连接P′A′,作CH⊥AB交AB的延长线于H.
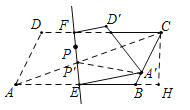
∵A、A′关于直线EF对称,
∴P′A′=P′A,
∴P′A′+P′C=P′A+P′C=AC,
∴当点P与P′重合时,PA′+PC的值最小,最小值=AC的长.
在Rt△BCH中,∵BC=4,∠CBH=60°,
∴BH=2,CH=2![]() ,
,
∴AH=AB+BH=10,
在Rt△ACH中,AC=![]() .
.
∴PC+PA′的最小值为![]() ,
,
故选:D.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
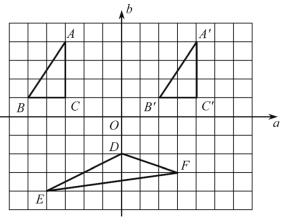
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的变换得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请求出三角形DEF的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
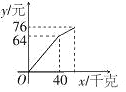
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
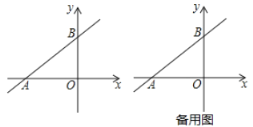
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且经过点
两点,且经过点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,
①求![]() 的值;
的值;
②点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 为坐标平面内另一点,若以
为坐标平面内另一点,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形,请直接写出所有符合条件的点
为顶点的四边形是菱形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
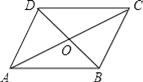
A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南山植物园中现有A、B两个园区,已知A园区为长方形,长为(x+y)米,宽为(x﹣y)米;B园区为正方形,边长为(x+3y)米.
(1)请用代数式表示A、B两园区的面积之和并化简;
(2)现根据实际需要对A园区进行整改,长增加(11x﹣y)米,宽减少(x﹣2y)米,整改后A区的长比宽多350米,且整改后两园区的周长之和为980米.
①求x、y的值;
②若A园区全部种植C种花,B园区全部种植D种花,且C、D两种花投入的费用与吸引游客的收益如表:

求整改后A、B两园区旅游的净收益之和.(净收益=收益﹣投入)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
①EG=DF;
②∠AEH+∠ADH=180°;
③△EHF≌△DHC;
④若 ![]() =
= ![]() ,则S△EDH=13S△CFH .
,则S△EDH=13S△CFH . 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com