
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且经过点
两点,且经过点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,
①求![]() 的值;
的值;
②点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 为坐标平面内另一点,若以
为坐标平面内另一点,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形,请直接写出所有符合条件的点
为顶点的四边形是菱形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①3;②
;(2)①3;②![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点(4,b+3)代入直线解析式中即可得出结论;
(2)①先求出点A,B坐标,进而得出AB,再利用AB=OB+2,即可求出b;
②分三种情况利用菱形的性质即可得出结论.
解:(1)直线y=kx+b经过点(4,b+3)
∴4k+b=b+3,
∴4k=3,
∴k=![]()
(2)①由(1)知A,B在y=![]() x+b上,
x+b上,
当x=0时,y=b, ∴B(0,b),
当y=0时,![]() x+b=0,解得x=
x+b=0,解得x=![]() ∴A(
∴A(![]() ,0),
,0),
∴OA=![]() ,OB=b
,OB=b
∴AB=![]()
∵AB=OB+2
∴![]() =b+2
=b+2
∴b=3
故答案为:3
②如图,由①知,b=3,∴A(-4,0),B(0,3) ∴AB=5
∵以A,B,M,N为顶点的四边形是菱形,
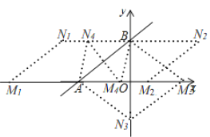
所以,分3种情况:
Ⅰ、当AB与AM为两邻边时,BN∥AM,BN=AM=AB=5,
∴N(-5,3)或(5,3)
Ⅱ、当AB与BM为两邻边时,AM和AN是对角线,∵B(0,3) ∴N(0,-3),
Ⅲ、当AM和AN为两邻边时,BN∥AM,
设N(n,3),∴BM=AM=BN=﹣n ∴OM=4+n,
根据勾股定理得,n2-(4+n)2=9,
n=﹣![]()
N(﹣![]() ,3)
,3)
故答案为:N(5,3)或(-5,3)或(0,-3)或(﹣![]() ,3)
,3)


科目:初中数学 来源: 题型:
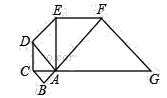
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五名同学在一次数学测验中的平均成绩是80分,而
五名同学在一次数学测验中的平均成绩是80分,而![]() ,
,![]() ,
,![]() 三人的平均成绩是78分,下列说法一定正确的是( )
三人的平均成绩是78分,下列说法一定正确的是( )
A.![]() ,
,![]() 两人的平均成绩是83分B.
两人的平均成绩是83分B.![]() ,
,![]() 的成绩比其他三人都好
的成绩比其他三人都好
C.五人成绩的中位数一定是80分D.五人的成绩的众数一定是80分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名队员参加射击训练,成绩分别被制成下列两个统计图:

根据以上信息,整理分析数据如下:
平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
甲 |
| 7 | 7 | 1.2 |
乙 | 7 |
| 8 | 4.2 |
(1)写出表格中![]() ,
,![]() 的值;
的值;
(2)从方差的角度看,若选派其中一名参赛,你认为应选哪名队员?并说明理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①):
①求证:△BOG≌△POE;②猜想:![]() = ;
= ;
(2)当点P与点C不重合时,如图②,![]() 的值会改变吗?试说明理由.
的值会改变吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线EF分别交平行四边形ABCD边AB、CD于直E、F,将图形沿直线EF对折,点A、D分別落在点A′、D′处.若∠A=60°,AD=4,AB=8,当点A′落在BC边上任意点时,设点P为直线EF上的动点,请直接写出PC+PA′的最小值( )
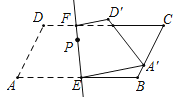
A.4+![]() B.8C.6+
B.8C.6+![]() D.4
D.4![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于![]() 的二次函数
的二次函数![]() 和
和![]() ,若
,若![]() 与
与![]() 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数![]() 的表达式,并求出当
的表达式,并求出当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com