
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①):
①求证:△BOG≌△POE;②猜想:![]() = ;
= ;
(2)当点P与点C不重合时,如图②,![]() 的值会改变吗?试说明理由.
的值会改变吗?试说明理由.

【答案】(1)①证明见解析;②![]() ;(2)
;(2)![]() ,不会改变,理由见解析.
,不会改变,理由见解析.
【解析】
(1)①由四边形ABCD是正方形,P与C重合,易证得OB=OP,∠BOC=∠BOG=90°,由同角的余角相等,证得∠GBO=∠EPO,则可利用ASA证得:△BOG≌△POE;
②先判断出∠BPF=∠GPF,进而得出BF=![]() BG,由①得△BOG≌△POE,得出BG=PE,即可得出结论;
BG,由①得△BOG≌△POE,得出BG=PE,即可得出结论;
(2)首先过P作PM∥AC交BG于M,交BO于N,易证得△BMN≌△PEN(ASA),△BPF≌△MPF(ASA),即可得BM=PE,BF=![]() BM.则可求得
BM.则可求得![]()
的值;
(1)①证明:∵四边形ABCD是正方形,P与C重合,
∴OB=OP,∠BOC=∠BOG=90°,
∵PF⊥BG,∠PFB=90°,
∴∠GBO=90°﹣∠BGO,∠EPO=90°﹣∠BGO,
∴∠GBO=∠EPO,
在△BOG和△POE中,
∵ ,
,
∴△BOG≌△POE(ASA);
②由①知,△BOG≌△POE,
∴BG=PE,
∵∠BPE=![]() ∠ACB,∠BPF+∠GPF=∠ACB,
∠ACB,∠BPF+∠GPF=∠ACB,
∴∠BPF=∠GPF,
∵BF⊥PE,
∴BF=![]() BG,
BG,
∴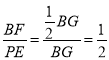 ,
,
故答案为![]() ;
;
(2)解:猜想![]() .
.
证明:如图2,过P作PM∥AC交BG于M,交BO于N,
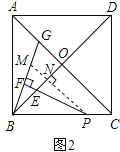
∴∠PNE=∠BOC=90°,∠BPN=∠OCB.
∵∠OBC=∠OCB=45°,
∴∠NBP=∠NPB.
∴NB=NP.
∵∠MBN=90°﹣∠BMN,∠NPE=90°﹣∠BMN,
∴∠MBN=∠NPE,
在△BMN和△PEN中,
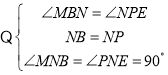 ,
,
∴△BMN≌△PEN(ASA),
∴BM=PE.
∵∠BPE=![]() ∠ACB,∠BPN=∠ACB,
∠ACB,∠BPN=∠ACB,
∴∠BPF=∠MPF.
∵PF⊥BM,
∴∠BFP=∠MFP=90°.
在△BPF和△MPF中,
 ,
,
∴△BPF≌△MPF(ASA).
∴BF=MF.
即BF=![]() BM.
BM.
∴BF=![]() PE.
PE.
即![]() =
=![]() .
.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )

A. 逐渐增加 B. 逐渐减小
C. 保持不变且与EF的长度相等 D. 保持不变且与AB的长度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
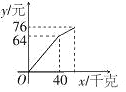
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.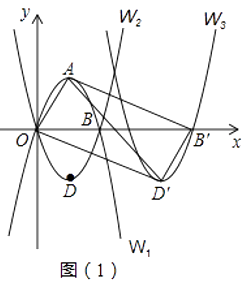
(1)求抛物线W2的解析式;
(2)将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.
(3)在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
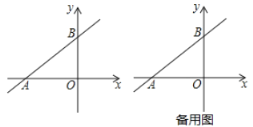
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,且经过点
两点,且经过点![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() ,
,
①求![]() 的值;
的值;
②点![]() 为
为![]() 轴上一动点,点
轴上一动点,点![]() 为坐标平面内另一点,若以
为坐标平面内另一点,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是菱形,请直接写出所有符合条件的点
为顶点的四边形是菱形,请直接写出所有符合条件的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
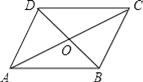
A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
(1)求证:∠BDC=∠A;
(2)若CE=2,DE=1,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“父亲节”的临近,某商场决定开展“感恩父爱,回馈顾客”的促销活动,对部分节日大礼包进行打折销售.其中![]() 款节日大礼包打
款节日大礼包打![]() 折
折![]() 款节日大礼包打
款节日大礼包打![]() 折.已知打折前,购买
折.已知打折前,购买![]() 盒
盒![]() 款节日大礼包和
款节日大礼包和![]() 盒
盒![]() 款节日大礼包需要
款节日大礼包需要![]() 元;打折后买
元;打折后买![]() 盒
盒![]() 款节日大礼包和
款节日大礼包和![]() 盒
盒![]() 款节日大礼包需要
款节日大礼包需要![]() 元.
元.
![]() 求打折后
求打折后![]() 两款节日大礼包每盒分别为多少元?
两款节日大礼包每盒分别为多少元?
![]() 打折期间,某公司计划为员工采购
打折期间,某公司计划为员工采购![]() 盒节日大礼包,总费用不超过
盒节日大礼包,总费用不超过![]() 元,则最多可以购买
元,则最多可以购买![]() 款节日大礼包多少盒?
款节日大礼包多少盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com