
【题目】观察下列等式:
①![]() ;②
;②![]() ;③
;③![]() ;…
;…
根据上述式子的规律,解答下列问题:
(1)第④个等式为 ;
(2)写出第![]() 个等式,并验证其正确性.
个等式,并验证其正确性.
【答案】(1)10×12+1=121;(2) 2n×(2n+2)+1=(2n+1)2
【解析】
(1)由已知等式知,两个连续偶数的积加上1,等于两连续偶数中间奇数平方,根据此规律写出即可;
(2)由(1)中规律可得第n个等式,再根据整式的运算即可验证.
解:(1)∵第①个等式为2×4+1=32,
第②个等式为4×6+1=25=52,
第③个等式为6×8+1=49=72,
∴第④个等式为10×12+1=112=121,
故答案为:10×12+1=121;
(2)由(1)知第n个等式为:2n×(2n+2)+1=(2n+1)2,
∵左边=4n2+4n+1=(2n+1)2=右边,
∴2n×(2n+2)+1=(2n+1)2.


科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置.此时AC′的中点恰好与点D重合,AB′交CD于点E,若AB=3,则△AEC的面积为( )
A.3
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日天气晴朗,某集团公司准备组织全体员工外出踏青.决定租用甲、乙、丙三种型号的巴士出行,甲型巴士每辆车的乘载量是乙型巴士的3倍,丙型巴士每辆可乘坐36人.现在旅游公司有甲、乙、丙型巴士若干辆,预计给该集团公司安排申型、丙型巴士共计8辆,其余员工安排乙型巴士,每辆巴士均满载,这样乘坐乙型巴士和丙型巴士的员工共296人.临行前,突然有若干人因特殊原因请假,这样一来刚好可以减少租用一辆乙型包士,且有一辆乙型巴士多出两个空位,这样甲、乙两种型号巴士共计装载178人;则该集团公司共有________名员工.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.
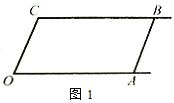
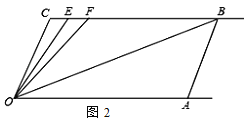
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2018个等腰直角三角形的斜边长是______.
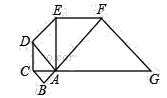
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB.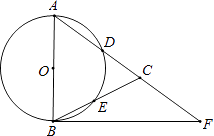
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
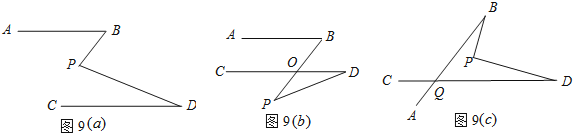
【题目】如图,平面内的直线有相交和平行两种位置关系.
(1)如图(a),已知AB∥CD,求证:∠BPD=∠B+∠D.
(2)如图(b),已知AB∥CD,求证:∠BOD=∠P+∠D.
(3)根据图(c),试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC、BD交于点O,点P在线段BC上(不含点B),∠BPE=![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
(1)当点P与点C重合时(如图①):
①求证:△BOG≌△POE;②猜想:![]() = ;
= ;
(2)当点P与点C不重合时,如图②,![]() 的值会改变吗?试说明理由.
的值会改变吗?试说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com