
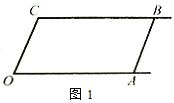
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
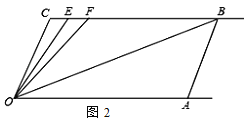
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.
【答案】(1)见解析;(2)①35°,②∠OBC:∠OFC的值不发生变化,∠OBC:∠OFC=1:2
【解析】试题分析:(1)由平行线的性质得到∠C+∠COA=180°,再由∠C=∠OAB,得到∠OAB+∠COA=180°,根据同旁内角互补,两直线平行即可得到结论;
(2)①先求出∠COA的度数,由∠FOB=∠AOB,OE平分∠COF, 即可得到结论;
②∠OBC:∠OFC的值不发生变化.由平行线的性质可得∠OBC=∠BOA,∠OFC=∠FOA.
由FOB=∠AOB,得到∠OFC=2∠OBC,从而得出结论.
试题解析:解:(1)∵CB∥OA, ∴∠C+∠COA=180°.
∵∠C=∠OAB,∴∠OAB+∠COA=180°,∴AB∥OC;
(2)①∠COA=180°-∠C=70°.∵∠FOB=∠AOB,OE平分∠COF, ∴ ∠FOB+∠EOF= (∠AOF+∠COF)= ∠COA=35°;
②∠OBC:∠OFC的值不发生变化.
∵CB∥OA,∴∠OBC=∠BOA,∠OFC=∠FOA.
∵∠FOB=∠AOB,∴∠FOA=2∠BOA,∴∠OFC=2∠OBC,∴∠OBC:∠OFC=1:2.


科目:初中数学 来源: 题型:
【题目】在学习“有理数加法“时,我们利用“(+5)+(+3)=+8,(-5)+(-3)=-8,……”抽象归纳推出了“同号两数相加,取相同的符号,并把绝对值相加”的加法法则.这种推导方法叫( )
A.排除法B.归纳法C.类比法D.数形结合法
查看答案和解析>>
科目:初中数学 来源: 题型:
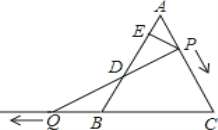
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)证明:在运动过程中,点D是线段PQ的中点;
(3)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,点E在直线DF上,点B在直线AC上,若∠AGB=∠EHF,∠C=∠D.
求证:∠A=∠F.

证明:∵∠AGB=∠EHF
∠AGB=___________(对顶角相等)
∴∠EHF=∠DGF
∴DB∥EC(____________________________________)
∴∠_________=∠DBA(________________________________)
又∵∠C=∠D
∴∠DBA=∠D
∴DF∥_______(__________________________________)
∴∠A=∠F(__________________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形OABC中,O为直角坐标系的原点,A、C两点的坐标分别为(6,0),(0,10),点B在第一象限内.
(1)写出点B的坐标,并求长方形OABC的周长;
(2)若有过点C的直线CD把长方形OABC的周长分成3:5两部分,D为直线CD与长方形的边的交点,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场家电专柜购进一批甲,乙两种电器,甲种电器共用了10 350元,乙种电器共用了9 600元,甲种电器的件数是乙种电器的1.5倍,甲种电器每件的进价比乙种电器每件的进价少90元.
(1)甲、乙两种电器各购进多少件?
(2)商场购进两种电器后,按进价提高40%后标价销售,很快全部售完,求售完这批电器商场共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查方式,你认为最合适的是( )
A.日光灯管厂要检测一批灯管的使用寿命,采用全面调查方式
B.旅客上飞机前的安检,采用抽样调查方式
C.了解深圳市居民日平均用水量,采用全面调查方式
D.了解深圳市每天的平均用电量,采用抽样调查方式
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
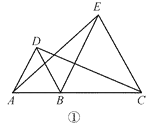
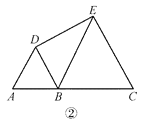
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
(2)如图②,若 AB=1,BC=2,求 DE 的长;
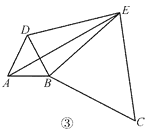
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com