
����Ŀ����ֱ����˳��ȡ A��B��C ���㣬�ֱ��� AB��BC Ϊ�߳���ֱ�ߵ�ͬ�����������Σ� ���������������ε���һ����ֱ�Ϊ D��E��
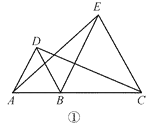
(1)��ͼ�٣����� CD��AE����֤��CD��AE��
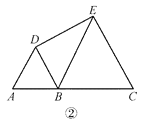
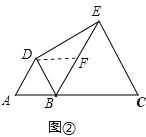
(2)��ͼ�ڣ��� AB��1��BC��2���� DE �ij���
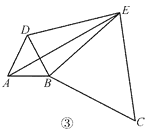
(3)��ͼ�ۣ���ͼ���е��������� BCE �� B �����ʵ�����ת������ AE������ DE2��BE2�� AE2�������DEB �Ķ�����
���𰸡�������
�������������������1������ABD����ECB���ǵȱ������οɵ�AD=AB=BD��BC=BE=EC����ABD=��EBC=60�������ԡ�ABE=��DBC��������ABE�ա�DBC������֤��AE=DC����2��
��ͼ���У�ȡBE�е�F������DF�������ⲻ�ѵó�BF=EF=1=BD���ٽ�ϡ�DBF=60���ɵ���DBF�ǵȱ������Σ������Ƴ���EDB=90�������ɹ��ɶ��������DE�ij�����3����ͼ���У�����DC������֪��������֤����ABE�ա�DBC������AE=DC����ΪDE2+BE2=AE2��BE=CE������DE2+CE2=CD2�����ԡ�DEC=90������Ϊ��BEC=60�������ԡ�DEB=��DEC����BEC=30����
���������
��1��֤������ͼ���У�
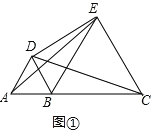
�ߡ�ABD����ECB���ǵȱ������Σ�
��AD=AB=BD��BC=BE=EC����ABD=��EBC=60����
���ABE=��DBC��
����ABE����DBC��
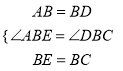 ��
��
���ABE�ա�DBC��
��AE=DC��
��2����ͼ���У�ȡBE�е�F������DF��
��BD=AB=1��BE=BC=2����ABD=��EBC=60����
��BF=EF=1=BD����DBF=60����
���DBF�ǵȱ���������
��DF=BF=EF����DFB=60����
�ߡ�BFD=��FED+��FDE��
���FDE=��FED=30����
���EDB=180������DBE����DEB=90����
��DE=![]() ��
��
��3����ͼ���У�����DC��
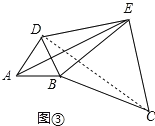
�ߡ�ABD�͡�ECB���ǵȱ������Σ�
��AD=AB=BD��BC=BE=EC����ABD=��EBC=60����
���ABE=��DBC��
�ڡ�ABE�͡�DBC�У�
 ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
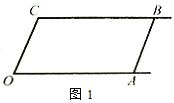
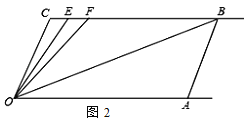
����Ŀ����ͼ1����֪����CB��OA����C=��OAB��
��1����֤��AB��OC��
��2����ͼ2��E��F��CB�ϣ��������FOB=��AOB��OEƽ�֡�COF.
�ٵ���C=110��ʱ�����EOB�Ķ���.
����ƽ���ƶ�AB����ô��OBC :��OFC��ֵ�Ƿ���֮�����仯�����仯���ҳ���
�����ɣ������䣬��������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����е��鷽ʽ�ʺ��ղ���ǣ� ��
A.һ���ڵ���ɱ����B.����Էϵ�صĴ������
C.�ɻ������������D.���꼶ѧ����ȫ֪ʶ����֪���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
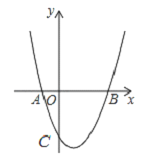
����Ŀ����ͼ����֪������y=x2+bx+c����A��-1��0����B��3��0�����㣬��C����������y��Ľ��㣮
��1���������ߵĽ���ʽ�Ͷ������ꣻ
��2����0��x��3ʱ����y��ȡֵ��Χ��
��3���������ߵĶԳ������Ƿ���ڵ�M��ʹ��BCM�ǵ��������Σ���������ֱ��д����M���꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ��� y��kx��4(k��0)��
(1)�� x����1 ʱ��y��2����˺����ı���ʽ��
(2)����ͼ���� x �ᡢy ��Ľ���ֱ�Ϊ A��B�� �����AOB �������
(3)����ͼ������� y��3 ʱ��x ��ȡֵ��Χ��
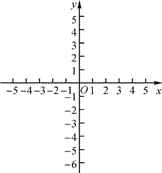
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����
��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ��3��
��3��
��![]() ����������Ϊ2��С������Ϊ
����������Ϊ2��С������Ϊ![]() ��2��
��2��
��1��![]() ��1��2
��1��2
��![]() ��1����������Ϊ1��
��1����������Ϊ1��
��![]() ��1��С������Ϊ
��1��С������Ϊ![]() ��2
��2
������⣺��֪��a��![]() ��3���������֣�b��
��3���������֣�b��![]() ��3��С�����֣�
��3��С�����֣�
��1��a��b��ֵ��
��2������a��3+��b+4��2��ƽ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
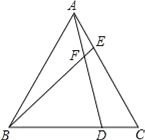
����Ŀ����ͼ����֪��ABCΪ�ȱ������Σ����������������Ϊ60���������Σ�����D��E�ֱ���BC��AC���ϣ���AE=CD��AD��BE�ཻ�ڵ�F��
��1����֤����ABE�ա�CAD��
��2�����BFD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��BC��CD��BC������ֱ�ΪB��C��AB=BC��EΪBC���е�����AE��BD��F����CD=4cm����AB�ij���Ϊ��������

A. 4cm B. 8cm C. 9cm D. 10cm
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com