
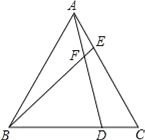
【题目】如图,已知△ABC为等边三角形(三条边相等三个角为60°的三角形),点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F.
(1)求证:△ABE≌△CAD;
(2)求∠BFD的度数.
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,AC=8cm,CB=6cm,点M、N分别是AC、BC的中点.
(1)求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a cm,其它条件不变,你能猜想MN的长度吗?并说明理由;
(3)若C在线段AB的延长线上,且满足AC﹣BC=b cm,M、N分别为AC、BC的中点,你能猜想MN的长度吗?并说明理由;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
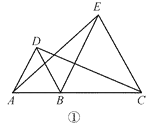
【题目】在直线上顺次取 A,B,C 三点,分别以 AB,BC 为边长在直线的同侧作正三角形, 作得两个正三角形的另一顶点分别为 D,E.
(1)如图①,连结 CD,AE,求证:CD=AE;
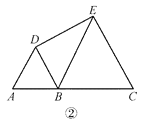
(2)如图②,若 AB=1,BC=2,求 DE 的长;
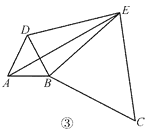
(3)如图③,将图②中的正三角形 BCE 绕 B 点作适当的旋转,连结 AE,若有 DE2+BE2= AE2,试求∠DEB 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品A的零售价为每件900元,为了适应市场竞争,商店按零售价的九折优惠后,再让利40元销售,仍可获利10%.
(1)这种商品A的进价为多少元?
(2)现有另一种商品B进价为600元,每件商品B也可获利10%.对商品A和B共进货100件,要使这100件商品共获纯利6670元,则需对商品A、B分别进货多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知将一块直角三角板DEF放置在△ABC上,使得该三角板的两条直角边DE,DF恰好分别经过点B、C.
(1)∠DBC+∠DCB= 度;
(2)过点A作直线直线MN∥DE,若∠ACD=20°,试求∠CAM的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB的端点坐标为A(2,-1),B(3,1).试画出AB向左平移4个单位长度的图形,写出A、B对应点C、D的坐标,并判断A、B、C、D四点组成的四边形的形状.(不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,对七年级男生进行引体向上测试.以做4个为标准,超过的个数记作正数,不足的个数记作负数其中8名男生做引体向上的个数记录如下:
+3 | -1 | 1 | +3 | 1 | 0 | +2 | -1 |
这8名男生平均每人做了多少个引体向上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com