
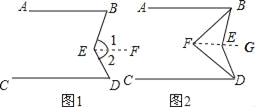
����Ŀ����֪��ֱ��AB��CD
��1����ͼ1����E��ֱ��BD����࣬�����ABE����CDE����BED��������ϵ����֤����Ľ��ۣ�
��2����ͼ2����E��ֱ��BD����࣬BF��DF�ֱ�ƽ�֡�ABE����CDE�������BFD�͡�BED��������ϵ����֤����Ľ��ۣ�
��3����ͼ3����E��ֱ��BD���Ҳ࣬BF��DF�ֱ�ƽ�֡�ABE����CDE����ô�ڣ�2�����С�BFD�͡�BED��������ϵ�IJ����Ƿ��Գ����������������֤�����������������д����IJ��룬��֤����



���𰸡���1����ABE+��CDE=��BED����2����BED=2��BFD����3��2��BFD+��BED=360�㣮
��������������(1)���ȹ���E��EF��AB,��֤�á�1=��ABE, ��2=��CDE,��ɵ�![]() .
.
(2)��������FE���ӳ�,��![]() ,����BF��DF�ֱ�ƽ�֡�ABE����CDE,�Լ�(1)�Ľ���,��֤�á�BED=2��BED;
,����BF��DF�ֱ�ƽ�֡�ABE����CDE,�Լ�(1)�Ľ���,��֤�á�BED=2��BED;
(3)��![]() ,�Լ�BF��DF�ֱ�ƽ�֡�ABE����CDE��
,�Լ�BF��DF�ֱ�ƽ�֡�ABE����CDE��![]() ,����֤�ý���.
,����֤�ý���.
���������
��1����ABE+��CDE=��BED��
֤��������E��EF��AB��
��AB��CD��
��EF��AB��CD��
���1=��ABE����2=��CDE��
���BED=��1+��2=��ABE+��CDE��
��2����BED=2��BFD��
֤��������FE���ӳ���
�ߡ�BEG=��BFE+��EBF����DEG=��DFE+��EDF��
���BED=��BFD+��EBF+��EDF��
��BF��DF�ֱ�ƽ�֡�ABE����CDE��
���ABE+��CDE=2����EBF+��EDF����
�ߡ�BED=��ABE+��CDE��
���EBF+��EDF=![]() ��BED��
��BED��
���BED=��BFD+![]() ��BED��
��BED��
���BED=2��BFD��
��3��2��BFD+��BED=360�㣮
��BF��DF�ֱ�ƽ�֡�ABE����CDE��
���ABF=![]() ��ABE����CDF=
��ABE����CDF=![]() ��CDE��
��CDE��
���ABF+��CDF=![]() ����ABE+��CDE����
����ABE+��CDE����
�ߡ�BFD=��ABF+��CDF=![]() ����ABE+��CDE����
����ABE+��CDE����
���ABE+��CDE=2��BFD��
�ߡ�BED+��BFD+��EBF+��EDF=360�㣬
��2��BFD+��BED=360�㣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
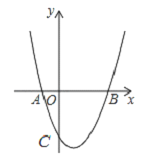
����Ŀ����ͼ����֪������y=x2+bx+c����A��-1��0����B��3��0�����㣬��C����������y��Ľ��㣮
��1���������ߵĽ���ʽ�Ͷ������ꣻ
��2����0��x��3ʱ����y��ȡֵ��Χ��
��3���������ߵĶԳ������Ƿ���ڵ�M��ʹ��BCM�ǵ��������Σ���������ֱ��д����M���꣬����������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
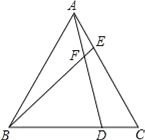
����Ŀ����ͼ����֪��ABCΪ�ȱ������Σ����������������Ϊ60���������Σ�����D��E�ֱ���BC��AC���ϣ���AE=CD��AD��BE�ཻ�ڵ�F��
��1����֤����ABE�ա�CAD��
��2�����BFD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ε����߳��ֱ�Ϊ5��7��������߳��������ǣ�������
A.2B.3C.10D.11
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC����AC��BC��10 cm��AB��12 cm����D��AB���е�������CD������P�ӵ�A��������A��C��B��·���˶��������Bʱ�˶�ֹͣ���ٶ�Ϊÿ��2 cm�����˶�ʱ��Ϊ![]() ����
����
��1����CD�ij���
��2����![]() Ϊ��ֵʱ����ADP��ֱ����������
Ϊ��ֵʱ����ADP��ֱ����������
��3��ֱ��д������![]() Ϊ��ֵʱ����ADP�ǵ�����������
Ϊ��ֵʱ����ADP�ǵ�����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦÿ��Ӽص��ҵض������壬�ס����������14ǧ�ף���֪�����е�ƽ���ٶ�Ϊ80��/�֣��ܲ���ƽ���ٶ�Ϊ200��/�֣�����Ҫ�ڲ�����10���ӵ�ʱ���ڴӼص����ҵأ�������Ҫ�ܲ����ٷ���?������Ҫ�ܲ�x���ӣ����г��IJ���ʽ�� ��
A.80x+200(10-x)��1.4B.80x+200(10-x)��1400
C.200x+80(10-x)��1.4D.200x+80(10-x)��1400
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��AB��BC��CD��BC������ֱ�ΪB��C��AB=BC��EΪBC���е�����AE��BD��F����CD=4cm����AB�ij���Ϊ��������

A. 4cm B. 8cm C. 9cm D. 10cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ע���ɣ�
��ͼ����֪��ֱ��AB��CD��ֱ��EF��GH���أ��ҡ�1=��2��
��˵������3+��4=180����
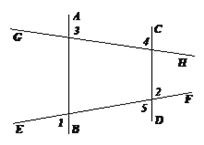
�⣺�ߡ�1=��2 ��______________��
�֡ߡ�2=��5 ��________��
���1=��5 ��________��
��AB��CD ��________��
���3+��4=180��________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��������x�ύ��A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��0��3����

��1���������ߵĽ���ʽ��
��2����x���·������������Ƿ����һ��P��ʹ��PAB�����������ABC������������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com