
【题目】如图,已知抛物线与x轴交于A(﹣1,0)、B(4,0)两点,与y轴交于点C(0,3).

(1)求抛物线的解析式;
(2)在x轴下方的抛物线上是否存在一点P,使△PAB的面积等于△ABC的面积?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=![]() (2)存在一点P,使△PAB的面积等于△ABC的面积
(2)存在一点P,使△PAB的面积等于△ABC的面积
【解析】试题分析:(1)设抛物线的解析式为y=ax2+bx+c,代入三点即求得方程式;
(2)由△ABC的底边AB上的高为3,设△PAB的高为h,则|h|=3,则点P的纵坐标为3或-3,然后根据点P在x轴的下方,可知纵坐标只能为-3,然后代入求解一元二次方程即可.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c,
∵抛物线与y轴交于点C的坐标(0,3),
∴y=ax2+bx+3,
又∵抛物线与x轴交于点A(﹣1,0)、B(4,0),
∴ ,
,
∴抛物线的解析式为![]() ;
;
(2)存在一点P,使△PAB的面积等于△ABC的面积,
∵△ABC的底边AB上的高为3,
设△PAB的高为h,则|h|=3,又点P在x轴下方,∴点P的纵坐标为﹣3,
![]() ,
,
∴点P的坐标为![]() ,
,![]() ,
,


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知,直线AB∥CD
(1)如图1,点E在直线BD的左侧,猜想∠ABE、∠CDE、∠BED的数量关系,并证明你的结论;
(2)如图2,点E在直线BD的左侧,BF、DF分别平分∠ABE、∠CDE,猜想∠BFD和∠BED的数量关系,并证明你的结论;
(3)如图3,点E在直线BD的右侧,BF、DF分别平分∠ABE、∠CDE;那么第(2)题中∠BFD和∠BED的数量关系的猜想是否仍成立?如果成立,请证明;如果不成立,请写出你的猜想,并证明.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在体育课上,对七年级男生进行引体向上测试.以做4个为标准,超过的个数记作正数,不足的个数记作负数其中8名男生做引体向上的个数记录如下:
+3 | -1 | 1 | +3 | 1 | 0 | +2 | -1 |
这8名男生平均每人做了多少个引体向上?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④∠DAE=∠DBC.其中正确的有( )

A. ②④ B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:
(1) 是描述小凡的运动过程(填![]() 或
或![]() );
);
(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)

查看答案和解析>>
科目:初中数学 来源: 题型:
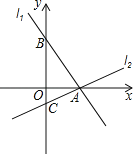
【题目】如图,过点A(2,0)的两条直线l1,l2分别交y轴于点B,C,其中点B在原点上方,点C在原点下方,已知AB=![]() .
.
(1)求点B的坐标;
(2)若△ABC的面积为4,求直线l2的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图锐角△ABC,若∠ABC=40°,∠ACB=70°,点D、E在边AB、AC上,CD与BE交于点H.
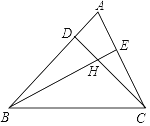
(1)若BE⊥AC,CD⊥AB,求∠BHC的度数.
(2)若BE、CD平分∠ABC和∠ACB,求∠BHC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
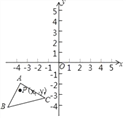
【题目】如图,△A′B′C′是△ABC经过平移得到的,△ABC三个顶点的坐标分别为A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4)
(1)请写出三角形ABC平移的过程;
(2)写出点A′,C′的坐标;
(3)求△A′B′C′的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com