Question

【题目】如图（1），抛物线W1：y=﹣x2+4x与x轴的正半轴交于点B，顶点为A，抛物线W2与W1关于x轴对称，顶点为D．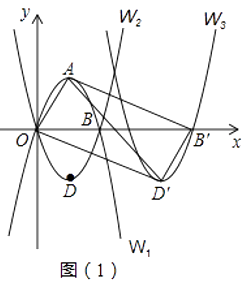

（1）求抛物线W2的解析式；
（2）将抛物线W2向右平移m个单位，点D的对应点为D′，点B的对应点为B′，则当m为何值时，四边形AOD′B′为矩形？请直接写出m的值．
（3）在（2）的条件下，将△AOD′沿x轴的正方向向右平移n个单位（0＜n＜5），得到△A′O′D′′，AD′分别与O′A′、O′D′′交于点M、点P，A′D′′分别与AB′、B′D′交于点N、点Q．
①求当n为何值时，四边形MNQP为菱形？
②若四边形MNQP的面积为S，求S关于n的函数关系式；并求当n为何值时，S的值最大？最大值为多少？

Answer 1

【答案】
（1）解：由y=﹣x2+4x=﹣（x﹣2）2+4得，点A坐标为（2，4），

∵抛物线W2与W1关于x轴对称，

∴点D坐标为（2，﹣4），

∴抛物线W2的解析式为y=（x﹣2）2﹣4，即y=x2﹣4x

（2）解：∵点A坐标为（2，4），

∴直线OA=2x，

∵点D坐标为（2，﹣4），

∴D′（2+m，﹣4），

∴直线OD′的解析式为y=﹣ x，

∵四边形AOD′B′为矩形，

∴AO⊥OD′，

∴2×（﹣ ）=﹣1，

∴m=6，

∴当m的值为6时，四边形AOD′B′为矩形

（3）解：①当y=0时，﹣x2+4x=0，解得x1=0，x2=4．

∴点B坐标为（4，0），

又∵m=6，

∴B′坐标为（10，0），

∴OB′=10；

设矩形AOD′B′的对角线AD′与OB′交于点E，A′D′′与x轴交于点F．．

∵四边形AOD′B′为矩形，

∴AE=OE=B′E=D′E=5，

∴∠OAE=∠AOE，∠EOD′=∠DOE．

∵A′O′∥AO，O′D′′∥OD′，

∴∠EMO′=∠MO′E，∠EO′P=∠EPO′，

∴ME=EO′=EP，

∵OE=5，OO′=n，

∴O′E=5﹣n，

∴ME=EP=5﹣n．

同理NF=FQ=FB′=5﹣n．

∵MP∥NQ，

∴四边形MEFN，EPQF为平行四边形．

∴MN∥EF∥PQ，

∴四边形MNQP为平行四边形，

∴当MN=MP时，四边形MNQP为菱形．

∵MN=AA′=n，MP=2O′E=10﹣2n．

∴n=10﹣2n．

解得n= ．

∴当n= 时，四边形MNQP为菱形；

②过M作MH⊥x轴，垂足为H，过A作AG⊥x轴，垂足为G，

则△MHE∽△AGE，

∴ ，

∴ = ，

∴MH= （5﹣n），

∴S=2S□MEFN=2× （5﹣n）﹣n=﹣ n2+8n，

∵S=﹣ （n﹣ ）2+10，∵﹣ ＜0，

∴当n= 时，S的值最大，最大值为10．

【解析】（1）抛物线关于x 轴对称与点的对称类似，横坐标不变，纵坐标变为其相反数，即-y=﹣x2+4x,y=x2-4x;（2）先求OA解析式，再用m的代数式表示直线OD′的解析式，根据矩形的性质，得出二直线互相垂直，即斜率之积为-1，求出m；（3）由已知可得四边形MNQP为平行四边形，若四边形MNQP为菱形须MN=MP，构建n的方程n=10﹣2n，求出ｎ；最值问题可运用函数思想，构建Ｓ关于ｎ的函数，二次函数可配成顶点式，求出最值．