
【题目】在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.

求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ① ),
∵ DE∥BC(已证),
∴ ② ( ③ ),
又∵∠1=∠2(已知),
∴ ④ ( ⑤ ),
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
【答案】①同位角相等,两直线平行;②∠1=∠DCB; ③两直线平行,内错角相等;④∠DCB=∠2 ;⑤等量代换.
【解析】
根据平行线的判定和性质解答即可.
∵∠ADE=∠B(已知),
∴DE∥BC( 同位角相等,两直线平行),
∵ DE∥BC(已证),
∴∠1=∠DCB ( 两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠DCB=∠2(等量代换),
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
故答案为:①同位角相等,两直线平行;②∠1=∠DCB; ③两直线平行,内错角相等;④∠DCB=∠2 ;⑤等量代换.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我国古代数字的许多创新和发展都位居世界前列,如南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”,根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为( )

A.2019B.2018C.191D.190
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型时尚![]() 恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的![]() 恤衫各购进多少件?
恤衫各购进多少件?
(2)商店进价提高50%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批![]() 恤衫商店共获利多少元?
恤衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
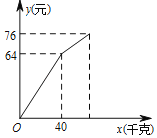
【题目】小华在暑假社会实践过程中,以每千克0.5元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示,请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的关系式?
(2)小华从批发市场共购进多少千克西瓜?
(3)小华这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
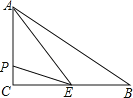
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以1cm/s的速度沿A→C运动,然后以2cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=__时,△APE的面积等于6 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )

A. 逐渐增加 B. 逐渐减小
C. 保持不变且与EF的长度相等 D. 保持不变且与AB的长度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,24,10分)某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.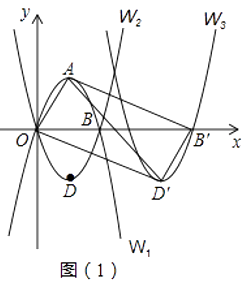
(1)求抛物线W2的解析式;
(2)将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.
(3)在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比特殊四边形的学习,我们可以定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.
(1)【探索体验】如图1,已知在四边形ABCD中,∠A=40°,∠B=100°,∠C=120°.求证:四边形ABCD是“等对角四边形”.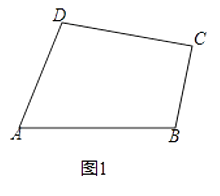
(2)如图2,若AB=AD=a,CB=CD=b,且a≠b,那么四边形ABCD是“等对角四边形”吗?试说明理由.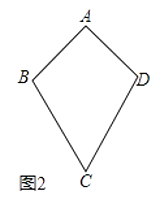
(3)【尝试应用】如图3,在边长为6的正方形木板ABEF上裁出“等对角四边形”ABCD,若已经确定DA=4m,∠DAB=60°,是否在正方形ABEF内(包括边上)存在一点C,使四边形ABCD以∠DAB=∠BCD为等对角的四边形的面积最大?若存在,试求出四边形ABCD的最大面积;若不存在,请说明理由.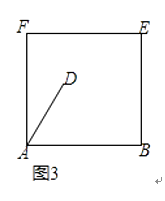
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com