
【题目】某服装店购进一批甲、乙两种款型时尚![]() 恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
恤衫,甲种款型共用了7800元,乙种款型共用了6400元.甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)甲、乙两种款型的![]() 恤衫各购进多少件?
恤衫各购进多少件?
(2)商店进价提高50%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型按标价的五折降价销售,很快全部售完,求售完这批![]() 恤衫商店共获利多少元?
恤衫商店共获利多少元?
【答案】(1)甲种款型的T恤衫购进60件,乙种款型的T恤衫购进40件;(2)售完这批T恤衫商店共获利4700元.
【解析】
(1)设乙种款型的T恤衫购进x件,则甲种款型的T恤衫购进1.5x件,根据单价=总价÷数量结合甲种款型每件的进价比乙种款型每件的进价少30元,即可得出关于x的分式方程,解之经检验即可得出结论;
(2)根据单价=总价÷数量可求出购进甲、乙两种款型T恤衫的单价,再根据利润=销售收入-成本,即可求出结论.
(1)设乙种款型的T恤衫购进x件,则甲种款型的T恤衫购进1.5x件,
根据题意:![]() ,
,
解得:x=40,
经检验,x=40是原方程的解,且符合题意,
∴1.5x=60.
答:甲种款型的T恤衫购进60件,乙种款型的T恤衫购进40件.
(2)6400÷40=160(元),160-30=130(元),
∴130×(1+50%)×60+160×(1+50%)×40×![]() +160×(1+50%)×
+160×(1+50%)×![]() ×40×
×40×![]() -7800-6400=4700(元).
-7800-6400=4700(元).
答:售完这批T恤衫商店共获利4700元.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】重庆不仅是网红城市,更是拥有长安,力帆等大型车企的一座汽车城,为了更好的推广和销售汽车,每年都会在悦来会展中心举办大型车展.去年该车展期间大众旗下两品牌汽车迈腾和途观L共计销售240辆,迈腾销售均价为每辆20万元,途观L销售均价为每辆30万元,两种车型去年车展期间销售额共计5600万元.
(1)这两种车型在去年车展期间各销售了多少辆?
(2)在今年的该车展上,各大汽车经销商纷纷采取降价促销手段,而途观L坚持不降价,与去年相比,销售均价不变,销量比去年车展期间减少了a%,而迈腾销售均价比去年降低了a%,销量较去年增加了2a%,两种车型今年车展期间销售总额与去年相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相较于点
相较于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() ,交
,交![]() 于
于![]() .
.
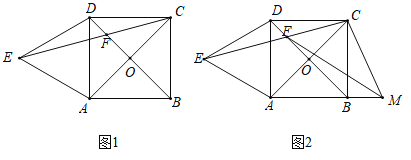
(1)如图1,若![]() ,求
,求![]() 的长
的长
(2)如图2,点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )

A. OE=![]() DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB.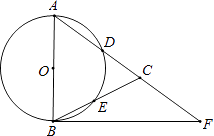
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
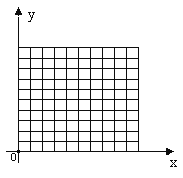
(1)填表:

(2)当P点从点O出发10秒,可得到的整数点的个数是 个.
(3)当P点从点O出发 秒时,可得到整数点(10 ,5).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列解题过程的空白处填上适当的推理理由或数学表达式:
如图,在△ABC中,已知∠ADE=∠B,∠1=∠2,FG⊥AB于点G.

求证:CD⊥AB.
证明:∵∠ADE=∠B(已知),
∴DE∥BC( ① ),
∵ DE∥BC(已证),
∴ ② ( ③ ),
又∵∠1=∠2(已知),
∴ ④ ( ⑤ ),
∴CD∥FG(同位角相等,两直线平行),
∴∠CDB=∠FGB(两直线平行,同位角相等),
∵ FG⊥AB(已知),
∴∠FGB=90°(垂直的定义).
∴∠CDB=90°
∴CD⊥AB(垂直的定义).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为矩形ABCD的对角线,AE⊥BD,垂足为E,tan∠BAE= ![]() ,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为 .
,BE=1,点P、Q分别在BD、AD上,连接AP、PQ,则AP+PQ的最小值为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com