
،¾جâؤ؟،؟£¨2011¹َضف°²ث³£¬24£¬10·ض£©ؤ³°àµ½±دزµت±¹²½لسà°à·ر1800شھ£¬°àخ¯»ل¾ِ¶¨ؤأ³ِ²»ةظسع270شھµ«²»³¬¹300شھµؤ×ت½ًخھہدت¦¹؛آٍ¼حؤîئ·£¬ئنسà×ت½ًسأسعشع±دزµحي»لةد¸ّ50خ»ح¬ر§أ؟بث¹؛آٍز»¼Tذô»ٍز»±¾س°¼¯×÷خھ¼حؤîئ·£®زرضھأ؟¼Tذô±بأ؟±¾س°¼¯¹َ9شھ£¬سأ200شھا،؛أ؟ةزشآٍµ½2¼Tذô؛ح5±¾س°¼¯£®
¢إاَأ؟¼Tذô؛حأ؟±¾س°¼¯µؤ¼غ¸ٌ·ض±ًخھ¶àةظشھ£؟
¢ئسذ¼¸ضض¹؛آٍTذô؛حس°¼¯µؤ·½°¸£؟
،¾´ً°¸،؟£¨1£©ةèTذô؛حس°¼¯µؤ¼غ¸ٌ·ض±ًخھ![]() شھ؛ح
شھ؛ح![]() شھ£®شٍ
شھ£®شٍ
![]()
½âµأ![]()
´ً£؛Tذô؛حس°¼¯µؤ¼غ¸ٌ·ض±ًخھ35شھ؛ح26شھ£®
£¨2£©ةè¹؛آٍTذô![]() ¼£¬شٍ¹؛آٍس°¼¯ (50-
¼£¬شٍ¹؛آٍس°¼¯ (50-![]() ) ±¾£¬شٍ
) ±¾£¬شٍ
![]()
½âµأ![]() £¬،ك
£¬،ك![]() خھصصûت£¬،à
خھصصûت£¬،à![]() = 23£¬24£¬25£¬
= 23£¬24£¬25£¬
¼´سذبضض·½°¸£®µعز»ضض·½°¸£؛¹؛Tذô23¼£¬س°¼¯27±¾£»
µع¶ضض·½°¸£؛¹؛Tذô24¼£¬س°¼¯26±¾£»
µعبضض·½°¸£؛¹؛Tذô25¼£¬س°¼¯25±¾£®
،¾½âخِ،؟آش


 تہ¼ح°ظح¨ئعؤ©½ً¾يدµءذ´ً°¸
تہ¼ح°ظح¨ئعؤ©½ً¾يدµءذ´ً°¸
| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعص·½ذخ![]() ضذ£¬¶ش½ادك
ضذ£¬¶ش½ادك![]() £¬
£¬![]() دà½دسعµم
دà½دسعµم![]() £¬زش
£¬زش![]() خھ±كدٍحâ×÷µب±ك
خھ±كدٍحâ×÷µب±ك![]() £¬ء¬½س
£¬ء¬½س![]() £¬½»
£¬½»![]() سع
سع![]() £®
£®
£¨1£©بçح¼1£¬بô![]() £¬اَ
£¬اَ![]() µؤ³¤
µؤ³¤
£¨2£©بçح¼2£¬µم![]() خھ
خھ![]() µؤرس³¤دكةدز»µم£¬ء¬½س
µؤرس³¤دكةدز»µم£¬ء¬½س![]() £¬ء¬½س
£¬ء¬½س![]() از
از![]() ئ½·ض
ئ½·ض![]() £®اَض¤£؛
£®اَض¤£؛![]() £®
£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµضذ£¬ةè×ّ±êضلµؤµ¥خ»³¤¶بخھ1cm£¬صûتµمP´سشµمO³ِ·¢£¬ثظ¶بخھ1cm/s£¬ازµمPض»ؤـدٍةد»ٍدٍسزشث¶¯£¬اë»ط´ًدآءذختجâ:
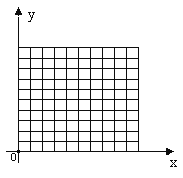
£¨1£©جî±ي£؛

£¨2£©µ±Pµم´سµمO³ِ·¢10أ룬؟ةµأµ½µؤصûتµمµؤ¸ِتتا ¸ِ£®
£¨3£©µ±Pµم´سµمO³ِ·¢ أëت±£¬؟ةµأµ½صûتµم£¨10 £¬5£©£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
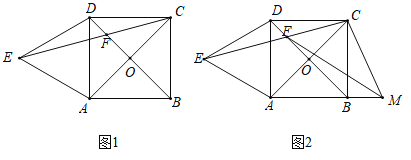
،¾جâؤ؟،؟شعدآءذ½âجâ¹³جµؤ؟ص°×´¦جîةدتتµ±µؤحئہيہيسة»ٍتر§±ي´ïت½£؛
بçح¼£¬شع،÷ABCضذ£¬زرضھ،دADE£½،دB£¬،د1£½،د2£¬FG،حABسعµمG£®

اَض¤£؛CD،حAB.
ض¤أ÷:،ك،دADE£½،دB£¨زرضھ£©£¬
،àDE،خBC£¨ ¢ظ £©£¬
،ك DE،خBC£¨زرض¤£©£¬
،à ¢ع £¨ ¢غ £©£¬
سض،ك،د1£½،د2£¨زرضھ£©£¬
،à ¢ـ £¨ ¢ف £©£¬
،àCD،خFG£¨ح¬خ»½ادàµب£¬ء½ض±دكئ½ذذ£©£¬
،à،دCDB£½،دFGB£¨ء½ض±دكئ½ذذ£¬ح¬خ»½ادàµب£©£¬
،ك FG،حAB£¨زرضھ£©£¬
،à،دFGB£½90،م£¨´¹ض±µؤ¶¨زه£©.
،à،دCDB£½90،م
،àCD،حAB£¨´¹ض±µؤ¶¨زه£©.
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بôxآْ×م![]() £¬اَ
£¬اَ![]() µؤضµ£®
µؤضµ£®
½â£؛ةè![]() £¬
£¬![]() £¬شٍ
£¬شٍ![]() £¬
£¬![]() £¬
£¬
ثùزش![]() =
=![]() =
=![]() =
=![]() =32-2،ء2=5£®
=32-2،ء2=5£®
اëشثسأةدأوµؤ·½·¨اَ½âدآأوµؤختجâ£؛
£¨1£©بô![]() آْ×م
آْ×م![]() £¬اَ
£¬اَ ![]() µؤضµ£»
µؤضµ£»
£¨2£©زرضھص·½ذخABCDµؤ±ك³¤خھ![]() £¬E،¢F·ض±ًتاAD،¢DCةدµؤµم£¬ازAE=1£¬CF=3£¬³¤·½ذخEMFDµؤأو»تا35£¬اَ³¤·½ذخEMFDµؤضـ³¤£®
£¬E،¢F·ض±ًتاAD،¢DCةدµؤµم£¬ازAE=1£¬CF=3£¬³¤·½ذخEMFDµؤأو»تا35£¬اَ³¤·½ذخEMFDµؤضـ³¤£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟(1)(5mn2©پ4m2n)(©پ2mn)£»،،،،(2)(a+b)2©پa(a+2b)£»
(3)(2a©پ1)(2a+1)©پa(4a©پ3)£» (4)©پ14+(2020©پ¦ذ)0©پ(©پ![]() )©پ2£»
)©پ2£»
(5)ہûسأ³ث·¨¹«ت½¼ٍ±م¼ئثم£؛20202-2019،ء2021£»
(6)دب»¯¼ٍ£¬شظاَضµ£؛[(5m©پ3n)(m+4n)©پ5m(m+4n)]،آ(-3n)£¬ئنضذm=2£¬n=©پ1£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ضذ؟¼جهس²âتشا°£¬ؤ³اّ½جس¾ضخھءثءث½âر،±¨زجهدٍةدµؤ³ُبؤذةْµؤ³ة¼¨اé؟ِ£¬ثو»ْ³éب،ءث±¾اّ²؟·ضر،±¨زجهدٍةددîؤ؟µؤ³ُبؤذةْµؤ³ة¼¨£¬²¢½«²âتشµأµ½µؤ³ة¼¨»و³ةءثدآأوء½·ù²»حêصûµؤح³¼ئح¼£؛

اëؤم¸ù¾فح¼ضذµؤذإد¢£¬½â´ًدآءذختجâ£؛
£¨1£©ذ´³ِةبذخح¼ضذ![]() ______£¬²¢²¹ب«جُذخح¼£»
______£¬²¢²¹ب«جُذخح¼£»
£¨2£©رù±¾ت¾فµؤئ½¾ùتتا______£¬ضعتتا______£¬ضذخ»تتا______£»
£¨3£©¸أاّجهسضذ؟¼ر،±¨زجهدٍةدµؤؤذةْ¹²سذ1200بث£¬بç¹ûجهسضذ؟¼زجهدٍةد´ï6¸ِزشةد£¨؛¬6¸ِ£©µأآْ·ض£¬اëؤم¹ہ¼ئ¸أاّجهسضذ؟¼ضذر،±¨زجهدٍةدµؤؤذةْؤـ»ٌµأآْ·ضµؤسذ¶àةظأû£؟
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬BDخھ¾طذخABCDµؤ¶ش½ادك£¬AE،حBD£¬´¹×مخھE£¬tan،دBAE= ![]() £¬BE=1£¬µمP،¢Q·ض±ًشعBD،¢ADةد£¬ء¬½سAP،¢PQ£¬شٍAP+PQµؤ×îذ،ضµخھ £®
£¬BE=1£¬µمP،¢Q·ض±ًشعBD،¢ADةد£¬ء¬½سAP،¢PQ£¬شٍAP+PQµؤ×îذ،ضµخھ £® 
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟بçح¼£¬شعئ½أوض±½ا×ّ±êدµضذ£¬´سµمP1£¨©پ1£¬0£©£¬P2£¨©پ1£¬©پ1£©£¬P3£¨1£¬©پ1£©£¬P4£¨1£¬1£©£¬P5£¨©پ2£¬1£©£¬P6£¨©پ2£¬©پ2£©£¬،زہ´خہ©ص¹دآب¥£¬شٍP2020µؤ×ّ±êخھ_____£®

²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com