
【题目】若x满足![]() ,求
,求![]() 的值.
的值.
解:设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
所以![]() =
=![]() =
=![]() =
=![]() =32-2×2=5.
=32-2×2=5.
请运用上面的方法求解下面的问题:
(1)若![]() 满足
满足![]() ,求
,求 ![]() 的值;
的值;
(2)已知正方形ABCD的边长为![]() ,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,求长方形EMFD的周长.
,E、F分别是AD、DC上的点,且AE=1,CF=3,长方形EMFD的面积是35,求长方形EMFD的周长.

科目:初中数学 来源: 题型:
【题目】如图,已知A是双曲线y= ![]() (k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移
(k>0)在第一象限内的一点,O为坐标原点,直线OA交双曲线于另一点C,当OA在第一象限的角平分线上时,将OA向上平移 ![]() 个单位后,与双曲线在第一象限交于点M,交y轴于点N,若
个单位后,与双曲线在第一象限交于点M,交y轴于点N,若 ![]() =2,
=2,
(1)求直线MN的解析式;
(2)求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
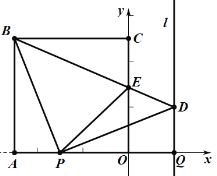
【题目】如图,正方形![]() 的边
的边![]() ,
,![]() 在坐标轴上,点
在坐标轴上,点![]() 的坐标为
的坐标为![]() .点
.点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴向点
轴向点![]() 运动;点
运动;点![]() 从点
从点![]() 同时出发,以相同的速度沿
同时出发,以相同的速度沿![]() 轴的正方向运动,规定点
轴的正方向运动,规定点![]() 到达点
到达点![]() 时,点
时,点![]() 也停止运动,连接
也停止运动,连接![]() ,过
,过![]() 点作
点作![]() 的垂线,与过点
的垂线,与过点![]() 平行于
平行于![]() 轴的直线
轴的直线![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,设点
,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)线段![]() (用含
(用含![]() 的式子表示),点
的式子表示),点![]() 的坐标为 (用含
的坐标为 (用含![]() 的式子表示),
的式子表示),![]() 的度数为 .
的度数为 .
(2)经探究![]() 周长是一个定值,不会随时间
周长是一个定值,不会随时间![]() 的变化而变化,请猜测周长的值并证明.
的变化而变化,请猜测周长的值并证明.
(3)①当![]() 为何值时,有
为何值时,有![]() .
.
②![]() 的面积能否等于
的面积能否等于![]() 周长的一半,若能求出此时
周长的一半,若能求出此时![]() 的长度;若不能,请说明理由.
的长度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
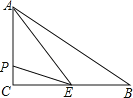
【题目】如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,点E是BC的中点,动点P从A点出发,先以1cm/s的速度沿A→C运动,然后以2cm/s的速度沿C→B运动.若设点P运动的时间是t秒,那么当t=__时,△APE的面积等于6 cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.

(1)试说明:∠BFD=∠ABC;
(2)若∠ABC=40°,EG∥AD,EH⊥BE,求∠HEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,24,10分)某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
在数学活动课上,老师给出如下问题,让同学们展开探究活动:
问题情境:
如图(1),在△ABC中,∠ACB=90°,AC=BC=a,点D为AB上一点(0<AD< ![]() AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.
AB),将线段CD绕点C逆时针旋转90°,得到的对应线段为CE,过点E作EF∥AB,交BC于点F.请你根据上述条件,提出恰当的数学问题并解答.
解决问题:
下面是学习小组提出的三个问题,请你解答这些问题:
(1)“兴趣”小组提出的问题是:求证:AD=EF.
(2)“实践”小组提出的问题是:如图(2),若将△ACD沿AB的垂直平分线对折,得到△BCG,连接EG,则线段EG与EF有怎样的数量关系?请说明理由.
(3)“奋进”小组在“实践”小组探究的基础上,提出了如下问题:延长EF与AC交于点H,连接HD,FG.求证:四边形DGFH是矩形.
提出问题:
(4)完成上述问题的探究后,老师让同学们结合图(3),提一个与四边形DGFH有关的问题.
“智慧”小组提出的问题是:当AD为何值时,四边形DGFH的面积最大?
请你参照智慧小组的做法,再提出一个与四边形DGFH有关的数学问题(提出问题即可,不要求进行解答,但所提问题必须有效)
你提出的问题是:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批篮球和足球,买1个篮球和2个足球共需170元,买2个篮球和1个足球共需190元.
(1)求一个篮球和一个足球的售价各是多少元?
(2)学校欲购进篮球和足球共100个,且足球数量不多于篮球数量的2倍,求出最多购买足球多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列推理证明.
如图,已知点D为BC延长线上一点,CE∥AB.
求证:∠A+∠B+∠ACB=180°

证明:∵CE∥AB,
∴∠1= ,( )
∠2= ,( )
又∠1+∠2+∠ACB=180°(平角的定义),
∴∠A+∠B+∠ACB=180°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com