
【题目】(1)(5mn2﹣4m2n)(﹣2mn); (2)(a+b)2﹣a(a+2b);
(3)(2a﹣1)(2a+1)﹣a(4a﹣3); (4)﹣14+(2020﹣π)0﹣(﹣![]() )﹣2;
)﹣2;
(5)利用乘法公式简便计算:20202-2019×2021;
(6)先化简,再求值:[(5m﹣3n)(m+4n)﹣5m(m+4n)]÷(-3n),其中m=2,n=﹣1.
【答案】(1)-10m2n3+8m3n2;(2)b2;(3)3a-1;(4)-4;(5)1;(6)m+4n,-2.
【解析】
(1)根据单项式乘以多项式的运算法则进行计算即可;
(2)先利用完全平方公式以及单项式乘以多项式的运算法则计算,再合并同类项即可;
(3)先利用平方差公式以及单项式乘以多项式的运算法则计算,再合并同类项即可;
(4)先利用乘方,零次幂以及负整指数幂的运算法则进行化简,再计算加减即可;
(5)先将2019×2021变形为(2020-1)×(2020+1),再利用平方差公式进行简便运算,从而可得出结果;
(6)先将原式中括号内的式子进行因式分解,再利用整式除法运算法则进行化简,最后将m,n的值代入即可得出结果.
解:(1)(5mn2﹣4m2n)(﹣2mn)=-10m2n3+8m3n2;
(2)(a+b)2﹣a(a+2b)=a2+2ab+b2-a2-2ab=b2;
(3)(2a﹣1)(2a+1)﹣a(4a﹣3)=4a2-1-4a2+3a=3a-1;
(4)﹣14+(2020﹣π)0﹣(﹣![]() )﹣2=-1+1-4=-4;
)﹣2=-1+1-4=-4;
(5)20202-2019×2021=20202-(2020-1)×(2020+1)=20202-20202+1=1;
(6)[(5m﹣3n)(m+4n)﹣5m(m+4n)]÷(-3n)=[(m+4n)(5m-3n-5m)]÷(-3n)=(m+4n)(-3n)÷(-3n)=m+4n,
将m=2,n=﹣1代入上式得,
原式=2+4×(-1)=-2.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,O为坐标原点,线段AB的两个端点A(0,2),B(1,0)分别在y轴和x轴的正半轴上,点C为线段AB的中点,现将线段BA绕点B按顺时针方向旋转90°得到线段BD,抛物线y=ax2+bx+c(a≠0)经过点D.
(1)如图1,若该抛物线经过原点O,且a=﹣ ![]() .
.
①求点D的坐标及该抛物线的解析式;
②连结CD,问:在抛物线上是否存在点P,使得∠POB与∠BCD互余?若存在,请求出所有满足条件的点P的坐标,若不存在,请说明理由;
(2)如图2,若该抛物线y=ax2+bx+c(a≠0)经过点E(1,1),点Q在抛物线上,且满足∠QOB与∠BCD互余.若符合条件的Q点的个数是3个,请直接写出a的值.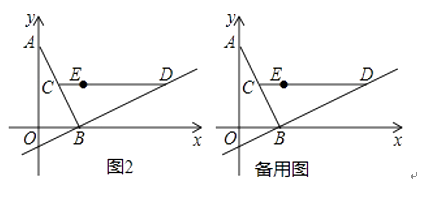
查看答案和解析>>
科目:初中数学 来源: 题型:
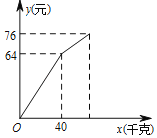
【题目】小华在暑假社会实践过程中,以每千克0.5元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示,请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的关系式?
(2)小华从批发市场共购进多少千克西瓜?
(3)小华这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,点E、F分别为AD、DC上的动点,∠EBF=60°,点E从点A向点D运动的过程中,AE+CF的长度( )

A. 逐渐增加 B. 逐渐减小
C. 保持不变且与EF的长度相等 D. 保持不变且与AB的长度相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011贵州安顺,24,10分)某班到毕业时共结余班费1800元,班委会决定拿出不少于270元但不超过300元的资金为老师购买纪念品,其余资金用于在毕业晚会上给50位同学每人购买一件T恤或一本影集作为纪念品.已知每件T恤比每本影集贵9元,用200元恰好可以买到2件T恤和5本影集.
⑴求每件T恤和每本影集的价格分别为多少元?
⑵有几种购买T恤和影集的方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
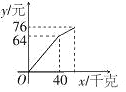
【题目】小明在暑期社会实践活动中,以每千克0.8元的价格从批发市场购进若干千克西瓜到市场上去销售,在销售了40千克西瓜之后,余下的每千克降价0.4元,全部售完.销售金额与售出西瓜的千克数之间的关系如图所示.请你根据图象提供的信息完成以下问题:
(1)求降价前销售金额y(元)与售出西瓜x(千克)之间的函数关系式.
(2)小明从批发市场共购进多少千克西瓜?
(3)小明这次卖瓜赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),抛物线W1:y=﹣x2+4x与x轴的正半轴交于点B,顶点为A,抛物线W2与W1关于x轴对称,顶点为D.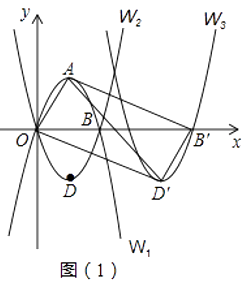
(1)求抛物线W2的解析式;
(2)将抛物线W2向右平移m个单位,点D的对应点为D′,点B的对应点为B′,则当m为何值时,四边形AOD′B′为矩形?请直接写出m的值.
(3)在(2)的条件下,将△AOD′沿x轴的正方向向右平移n个单位(0<n<5),得到△A′O′D′′,AD′分别与O′A′、O′D′′交于点M、点P,A′D′′分别与AB′、B′D′交于点N、点Q.
①求当n为何值时,四边形MNQP为菱形?
②若四边形MNQP的面积为S,求S关于n的函数关系式;并求当n为何值时,S的值最大?最大值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是( )
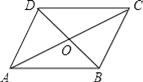
A. 1<m<11 B. 2<m<22 C. 10<m<12 D. 5<m<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com