【题目】如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，则tan∠ECF=（ ）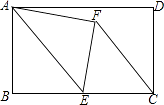
A.
B.
C.
D.
【答案】B
【解析】解：∵BC=12，点E是BC的中点，
∴EC=BE=6，
由翻折变换的性质可知，BE=FE，∠BEA=∠FEA，
∴EF=EC，
∴∠EFC=∠ECF，
∵∠BEA+∠FEA=∠EFC+∠ECF，
∴∠BEA=∠ECF，
∵tan∠BEA= 
= 
，
∴tan∠ECF= ，
所以答案是：B．
【考点精析】解答此题的关键在于理解三角形的外角的相关知识，掌握三角形一边与另一边的延长线组成的角，叫三角形的外角；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角，以及对翻折变换（折叠问题）的理解，了解折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等．
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目：初中数学 来源： 题型：
【题目】如图，数轴上点
表示的数为6，点
位于点的左侧，
，动点
从点出发，以每秒3个单位长度的速度沿数轴向左运动，动点
从点出发，以每秒2个单位长度的速度沿数轴向右运动．
（1）点表示的数是多少？
（2）若点，同时出发，求：
①当点与相遇时，它们运动了多少秒？相遇点对应的数是多少？
②当
个单位长度时，它们运动了多少秒？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是一个长为
、宽为
的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成一个“回形”正方形（如图2）
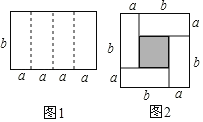
（1）观察图2请你写出
之间的等量关系是________；
（2）根据（1）中的结论，若
，则
________；
（3）拓展应用：若
，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，将Rt△ABC绕直角顶点B逆时针旋转90°得到△DBE，DE的延长线恰好经过AC的中点F，连接AD，CE．
（1）求证：AE＝CE；
（2）若BC＝
，求AB的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在平面直角坐标系中，
的顶点坐标分别
，现将先向右平移6个单位长度，再向下平移5个单位长度，得到
．
（1）直接写出点
的坐标；
（2）在平面直角坐标中画出，并求出的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y= 
的图象经过A，B两点，则菱形ABCD的面积为（ ）
A.2
B.4
C.2 
D.4
查看答案和解析>>
科目：初中数学 来源： 题型：
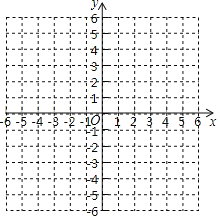
【题目】如图，已知平面直角坐标系中，A点坐标为（﹣4，4），B（﹣4，0）C（1，3），解答下列各题：
（1）按题中所给坐标在图中画出△ABC并直接写出△ABC的面积；
（2）画出△ABC先向右平移5个单位长度再向下平移3个单位长度的△A'B'C'，并直接写出A'，B′，C'的坐标；
（3）直接写出△ABC按照（2）问要求平移到△A'B'C'的过程中，△ABC所扫过的图形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）如图1，等腰
和等腰
中，
，
，
，
三点在同一直线上，求证：
；
（2）如图2，等腰中，
，
，是三角形外一点，且，求证：
；
（3）如图3，等边中，是形外一点，且
，
①
的度数为 ；
②
，
，
之间的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
