
【题目】如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为3,1,反比例函数y= ![]() 的图象经过A,B两点,则菱形ABCD的面积为( )
的图象经过A,B两点,则菱形ABCD的面积为( )
A.2
B.4
C.2 ![]()
D.4 ![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】南通某校为了了解家长和学生参与南通安全教育平台“![]() 防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下
防灾减灾”专题教育活动的情况,在本校学生中随机抽取部分学生做调查,把收集的数据分为以下![]() 类情形:
类情形:
A.仅学生自己参与;
B.家长和学生一起参与;
C.仅家长参与;
D.家长和学生都未参与
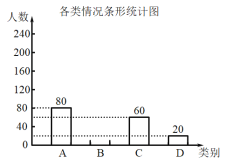
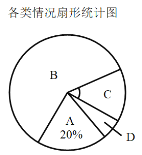
请根据上图中提供的信息,解答下列问题:
(1)在这次抽样调查中,共调查了多少名学生?
(2)补全条形统计图,并在扇形统计图中计算![]() 类所对应扇形的圆心角的度数;
类所对应扇形的圆心角的度数;
(3)根据抽样调查结果,估计该校![]() 名学生中“家长和学生都未参与”的人数.
名学生中“家长和学生都未参与”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )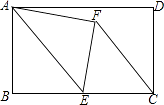
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+”是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(1)求点A(![]() ,
, ![]() )的勾股值[A],
)的勾股值[A],
(2)若将点A向上平移3个单位,再向左平移2个单位后得到点B,请直接写出点B的坐标,并求出点B的勾股值 [B];
(3)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为边长为1的正方形ABCD中CD边上的一动点(不含点C、D),以BE为边作图中所示的正方形BEFG.
(1)求∠ADF的度数;
(2)如图2,若BF交AD于点H,连接EH,求证:HB平分∠AHE;
(3)如图3,连接AE、CG,作BM⊥AE于点M,BM交GC于点N,连接DN.当E在CD上运动时,求证:NC=NG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有正方形ABCD和一个以O为直角顶点的三角板,移动三角板,使三角板两直角边所在直线分别与直线BC,CD交于点M、N.
(1)如图1,若点O与点A重合,则OM与ON的数量关系是;
(2)如图2,若点O在正方形的中心(即两对角线交点),则(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若点O在正方形的内部(含边界),当OM=ON时,请探究点O在移动过程中可形成什么图形?
(4)如图4,是点O在正方形外部的一种情况.当OM=ON时,请你就“点O的位置在各种情况下(含外部)移动所形成的图形”提出一个正确的结论.(不必说明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com