练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】有筐白菜,以每筐千克为标准,超过或不足的分别用正、负来表示,记录如下：

    与标准质量的差单位：千克

    筐 数

    (1)与标准质量比较,筐白菜总计超过或不足多少千克？

    (2)若白菜每千克售价元,则出售这筐白菜可卖多少元？

    【答案】（1）20筐白菜总计超出8千克；（2）出售这20筐白菜可卖1320.8元

    【解析】

    （1）根据有理数的运算，可得20筐白菜总计超过或不足多少千克；

    （2）根据单价×数量=总价的关系，可得总价．

    （1）由题意可得：

    -3×1+（-2）×4+（-1.5）×2+0×3+1×2+2.5×8=8（千克）

    答：20筐白菜总计超出8千克.

    （2）由（1）得：20×25+8=508（千克）508×2.6=1320.8（元）

    答：出售这20筐白菜可卖1320.8元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一列从小到大，按某种规律排列的数如下：，3，7，□，15，19，23，□，31，35，□，…，第（为正整数）个数记作，是的函数，则的值可能是下列个数中的（ ）．

    A.158B.124C.79D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC是等边三角形，点D，E分别在边BC，AC上，且CD=CE，连接DE并延长至点F，使EF=AE，连接AF，CF，连接BE并延长交CF于点G．下列结论：
    ①△ABE≌△ACF；②BC=DF；③S△ABC=S△ACF+S△DCF；④若BD=2DC，则GF=2EG．其中正确的结论是 ． （填写所有正确结论的序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax2﹣10ax+c经过点C，顶点M在直线BC上．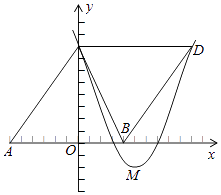

    （1）证明四边形ABCD是菱形，并求点D的坐标；
    （2）求抛物线的对称轴和函数表达式；
    （3）在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，菱形ABCD在第一象限内，边BC与x轴平行，A，B两点的纵坐标分别为3，1，反比例函数y= 的图象经过A，B两点，则菱形ABCD的面积为（ ）

    A.2
    B.4
    C.2
    D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCB1中，AB=1，AB与直线l的夹角为30°，延长CB1交直线l于点A1 ， 作正方形A1B1C1B2 ， 延长C1B2交直线l于点A2 ， 作正方形A2B2C2B3 ， 延长C2B3交直线l于点A3 ， 作正方形A3B3C3B4 ， …，依此规律，则A2016A2017= ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB∥CD，CF平分∠ECD，HC⊥CF交直线AB于H，AG平分∠HAE交HC于G，EJ∥AG交CF于J，∠AEC＝80°，则下列结论正确的有（　　）个．

    ①∠BAE+∠ECD＝80°；②CG平分∠ICE；③∠AGC＝140°；④∠EJC﹣∠AGH＝90°．

    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=﹣ x2+bx+e与x轴交于点A（﹣3，0）、点B（9，0），与y轴交于点C，顶点为D，连接AD、DB，点P为线段AD上一动点．
    （1）求抛物线的解析式；
    （2）如图1，过点P作BD的平行线，交AB于点Q，连接DQ，设AQ=m，△PDQ的面积为S，求S关于m的函数解析式，以及S的最大值；

    （3）如图2，抛物线对称轴与x轴交与点G，E为OG的中点，F为点C关于DG对称的对称点，过点P分别作直线EF、DG的垂线，垂足为M、N，连接MN，直接写出△PMN为等腰三角形时点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】观察图中给出的信息，回答下列问题：

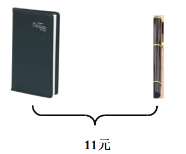
    （1）一本笔记本与一支中性笔分别是多少元？

    （2）某学校给参加体育比赛获一等奖的10名学生发笔记本，给获二等奖的20名学生发中性笔，现有两个超市在搞促销活动，A超市规定：这两种商品都打八折；B超市规定：每买一个笔记本送一支中性笔，另外购买的中性笔按原价卖．该学校选择哪家超市购买更合算，并说明理由．

    查看答案和解析>>

    同步练习册答案