
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.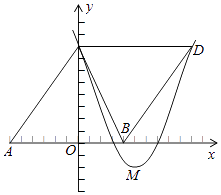
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
【答案】
(1)证明:∵A(﹣6,0),B(4,0),C(0,8),
∴AB=6+4=10,AC= ![]() =10,
=10,
∴AB=AC,
由翻折可得,AB=BD,AC=CD,
∴AB=BD=CD=AC,
∴四边形ABCD是菱形,
∴CD∥AB,
∵C(0,8),
∴点D的坐标是(10,8)
(2)解:∵y=ax2﹣10ax+c,
∴对称轴为直线x=﹣ ![]() =5.
=5.
设M的坐标为(5,n),直线BC的解析式为y=kx+b,
∴ ![]() ,
,
解得 ![]() .
.
∴y=﹣2x+8.
∵点M在直线y=﹣2x+8上,
∴n=﹣2×5+8=﹣2.
又∵抛物线y=ax2﹣10ax+c经过点C和M,
∴ ![]() ,
,
解得 ![]() .
.
∴抛物线的函数表达式为y= ![]() x2﹣4x+8
x2﹣4x+8
(3)解:存在.
理由如下:由题意可知,P在抛物线y= ![]() x2﹣4x+8上,且到BD,CD所在直线距离相等,所以P在二次函数与BD、CD所在的直线的夹角平分线的交点上,而BD、CD所在的直线的夹角平分线有两条:一条是AD所在的直线,解析式为y=
x2﹣4x+8上,且到BD,CD所在直线距离相等,所以P在二次函数与BD、CD所在的直线的夹角平分线的交点上,而BD、CD所在的直线的夹角平分线有两条:一条是AD所在的直线,解析式为y= ![]() x+3,另外一条是过D且与BC平行的直线,解析式为y=﹣2x+28,
x+3,另外一条是过D且与BC平行的直线,解析式为y=﹣2x+28,
联立 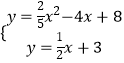 ,
,
解得: ![]() (舍)或
(舍)或 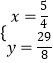 ,
,
联立 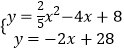 ,
,
解得: ![]() (舍)或
(舍)或 ![]()
所以当△PBD与△PCD的面积相等,点P的坐标为P1( ![]() ,
, ![]() ),P2(﹣5,38)
),P2(﹣5,38)
【解析】(1)根据两点之间的距离公式,勾股定理,翻折的性质得AB=BD=CD=AC,根据菱形的性质和判定得出D点的坐标;(2)根据对称轴公式得出抛物线的对称轴,设M的坐标为(5,n),直线BC的解析式为y=kx+b,根据待定系数法可得出M点的坐标,再根据待定系数法求出抛物线的解析式;(3)分点P在CD的上面和点P在CD的下面两种情况,根据等底等高的三角形面积相等即可求出P点的坐标。
【考点精析】认真审题,首先需要了解勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A(﹣2,m),B
的图象交于A(﹣2,m),B
(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
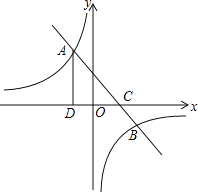
(1)求这两个函数的解析式:
(2)求△ADC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.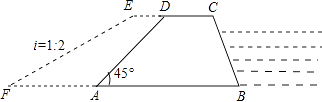
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,且BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/秒;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/秒,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
(1)当t为何值时,四边形PQCM是平行四边形?
(2)设四边形PQCM的面积为y(cm2),求y与t之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 筐白菜,以每筐
筐白菜,以每筐![]() 千克为标准,超过或不足的分别用正、负来表示,记录如下:
千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差 |
|
|
|
|
|
|
筐 数 |
|
|
|
|
|
|
(1)与标准质量比较,![]() 筐白菜总计超过或不足多少千克?
筐白菜总计超过或不足多少千克?
(2)若白菜每千克售价![]() 元,则出售这
元,则出售这![]() 筐白菜可卖多少元?
筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,台风中心位于点![]() ,并沿东北方向
,并沿东北方向![]() 移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,
移动,已知台风移动的速度为40千米/时,受影响区域的半径为260千米,![]() 市位于点
市位于点![]() 的北偏东75°方向上,距离
的北偏东75°方向上,距离![]() 点480千米.
点480千米.

(1)说明本次台风是否会影响![]() 市;
市;
(2)若这次台风会影响![]() 市,求
市,求![]() 市受台风影响的时间.
市受台风影响的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com