Question

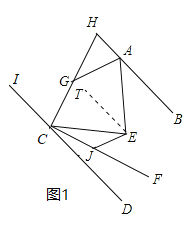
【题目】如图，AB∥CD，CF平分∠ECD，HC⊥CF交直线AB于H，AG平分∠HAE交HC于G，EJ∥AG交CF于J，∠AEC＝80°，则下列结论正确的有（　　）个．

①∠BAE+∠ECD＝80°；②CG平分∠ICE；③∠AGC＝140°；④∠EJC﹣∠AGH＝90°．

A.1B.2C.3D.4

Answer 1

【答案】D

【解析】

作ET∥BH，如图1，由平行公理的推论可得ET∥CD，然后利用平行线的性质和角的和差即可判断①；

由垂直的定义可得∠ECH+∠ECF＝90°，然后根据平角的定义和角平分线的定义即可判断②；

同①的方法可得∠AGC＝∠GAH+∠GCI，然后根据角平分线的定义和①的结论即可判断③；

延长HC交EJ的延长线于R，如图2，由平行线的性质可得∠AGH＝∠R，然后根据三角形的外角性质和已知条件HC⊥CF即可判断④．

解：作ET∥BH，如图1，则∠BAE＝∠AET，

∵DC∥BH，

∴ET∥CD，

∴∠ECD＝∠CET，

∴∠AEC＝∠AET+∠CET＝∠BAE+∠ECD＝80°，故①正确；

∵HC⊥CF，

∴∠ECH+∠ECF＝90°，∠FCD+∠HCI＝90°，

∵∠ECF＝∠FCD，

∴∠ECH＝∠HCI，

∴CH平分∠ECI，故②正确；

同①的方法可证：∠AGC＝∠GAH+∠GCI＝（∠EAH+∠ECI）＝（360°﹣∠BAE﹣∠ECD）＝（360°﹣80°）＝140°，故③正确；

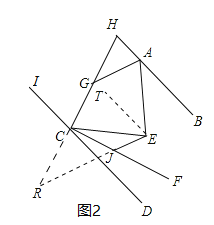
延长HC交EJ的延长线于R，如图2，

∵AG∥ER，

∴∠AGH＝∠R，

∵∠EJC＝∠R+∠RCJ，∠RCJ＝90°，

∴∠EJC﹣∠AGH＝90°，故④正确．

故选：D．