
【题目】如图,已知A,B是反比例函数y= ![]() (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
(k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C,动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C,过P作PM⊥x轴,垂足为M.设三角形OMP的面积为S,P点运动时间为t,则S关于t的函数图象大致为( )
A.
B.
C.
D.
【答案】A
【解析】解:设∠AOM=α,点P运动的速度为a,
当点P从点O运动到点A的过程中,S= ![]() =
= ![]() a2cosαsinαt2,
a2cosαsinαt2,
由于α及a均为常量,从而可知图象本段应为抛物线,且S随着t的增大而增大;
当点P从A运动到B时,由反比例函数性质可知△OPM的面积为 ![]() k,保持不变,
k,保持不变,
故本段图象应为与横轴平行的线段;
当点P从B运动到C过程中,OM的长在减少,△OPM的高与在B点时相同,
故本段图象应该为一段下降的线段;
所以答案是:A.
【考点精析】认真审题,首先需要了解反比例函数的性质(性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大).


科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,CF平分∠ECD,HC⊥CF交直线AB于H,AG平分∠HAE交HC于G,EJ∥AG交CF于J,∠AEC=80°,则下列结论正确的有( )个.
①∠BAE+∠ECD=80°;②CG平分∠ICE;③∠AGC=140°;④∠EJC﹣∠AGH=90°.

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在四边形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长,分别与
并延长,分别与![]() 、
、![]() 的延长线交于点
的延长线交于点![]() 、
、![]() ,证明:
,证明:![]() .
.
请将证明![]() 的过程填写完整:
的过程填写完整:
证明:连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() .
.
![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 的中点,
的中点,
![]() ________,
________,![]() _______,同理:
_______,同理:![]() _______,
_______,![]() _______,
_______,
![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,![]() ,
,![]() .
.
(2)运用上题方法解决下列问题:
问题一:如图2,在四边形![]() 中,
中,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,请判断
,请判断![]() 的形状,并说明理由;
的形状,并说明理由;
问题二:如图3,在钝角![]() 中,
中,![]() ,
,![]() 点在
点在![]() 上,
上,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,连接
的中点,连接![]() 并延长,与
并延长,与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 是直角三角形且
是直角三角形且![]() ,求证:
,求证:![]() .
.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”.比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则恰好小红抽中“唐诗”且小明抽中“宋词”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察图中给出的信息,回答下列问题:
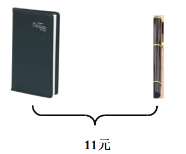

(1)一本笔记本与一支中性笔分别是多少元?
(2)某学校给参加体育比赛获一等奖的10名学生发笔记本,给获二等奖的20名学生发中性笔,现有两个超市在搞促销活动,A超市规定:这两种商品都打八折;B超市规定:每买一个笔记本送一支中性笔,另外购买的中性笔按原价卖.该学校选择哪家超市购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:材料一:对于任意的非零实数![]() 和正实数
和正实数![]() ,如果满足
,如果满足![]() 是整数,则称
是整数,则称![]() 是
是![]() 的一个“整商系数”, 例如:
的一个“整商系数”, 例如:![]() 时
时![]() ,则
,则![]() 是
是![]() 的一个“整商系数”;
的一个“整商系数”;![]() 时,
时,![]() ,则
,则![]() 也是
也是![]() 的一个“整商系数”;
的一个“整商系数”;
结论:一个非零实数有无数个整商系数![]() ,其中最小的一个整商系数记为
,其中最小的一个整商系数记为![]() ,例如:
,例如:![]() .
.
材料二:对于一元二次方程![]() 中,两根
中,两根![]() 有如下关系:
有如下关系:![]() , 应用:
, 应用:
(1)若实数![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)关于![]() 的方程
的方程![]() 的两个根分别为
的两个根分别为![]() ,且满足
,且满足![]() , 则
, 则![]() 的值为多少?
的值为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com