
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΗω≈ζΖΔΒξœζ έΆ§“Μ÷÷ΤΜΙϊΘ§‘ΎΦΉ≈ζΖΔΒξΘ§≤Μ¬έ“Μ¥ΈΙΚ¬ρ ΐΝΩ «Εύ…ΌΘ§ΦέΗώΨυΈΣ5‘Σ/![]() Θ°‘Ύ““≈ζΖΔΒξΘ§“Μ¥ΈΙΚ¬ρ ΐΝΩ≤Μ≥§Ιΐ
Θ°‘Ύ““≈ζΖΔΒξΘ§“Μ¥ΈΙΚ¬ρ ΐΝΩ≤Μ≥§Ιΐ![]() ±Θ§ΦέΗώΈΣ7‘Σ/
±Θ§ΦέΗώΈΣ7‘Σ/![]() ΘΜ“Μ¥ΈΙΚ¬ρ ΐΝΩ≥§Ιΐ
ΘΜ“Μ¥ΈΙΚ¬ρ ΐΝΩ≥§Ιΐ![]() ±Θ§Τδ÷–”–
±Θ§Τδ÷–”–![]() ΒΡΦέΗώΈΣ6‘Σ/
ΒΡΦέΗώΈΣ6‘Σ/![]() Θ§≥§Ιΐ
Θ§≥§Ιΐ![]() ≤ΩΖ÷ΒΡΦέΗώΈΣ4‘Σ/
≤ΩΖ÷ΒΡΦέΗώΈΣ4‘Σ/![]() Θ°…η–Γ’≈‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩΈΣ
Θ°…η–Γ’≈‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩΈΣ![]() Θ°
Θ°
Θ®1Θ©ΗυΨίΧβ“βΧν±μΘΚ
“Μ¥ΈΙΚ¬ρ ΐΝΩ/ | 20 | 50 | 150 | Γ≠ |
ΦΉ≈ζΖΔΒξΜ®Ζ―/‘Σ | 250 | Γ≠ | ||
““≈ζΖΔΒξΜ®Ζ―/‘Σ | 350 | Γ≠ |
Θ®2Θ©…η‘ΎΦΉ≈ζΖΔΒξΜ®Ζ―![]() ‘ΣΘ§‘Ύ““≈ζΖΔΒξΜ®Ζ―
‘ΣΘ§‘Ύ““≈ζΖΔΒξΜ®Ζ―![]() ‘ΣΘ§Ζ÷±π«σ
‘ΣΘ§Ζ÷±π«σ![]() Θ§
Θ§![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡΚ· ΐΫβΈω ΫΘΜ
ΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®3Θ©ΗυΨίΧβ“βΧνΩ’ΘΚ
ΔΌ»τ–Γ’≈‘ΎΦΉ≈ζΖΔΒξΚΆ‘Ύ““≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩœύΆ§Θ§«“Μ®Ζ―œύΆ§Θ§‘ρΥϊ‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩΈΣ_________![]() ΘΜ
ΘΜ
ΔΎ»τ–Γ’≈‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩΈΣ![]() Θ§‘ρΥϊ‘ΎΦΉΓΔ““ΝΫΗω≈ζΖΔΒξ÷–ΒΡ___________≈ζΖΔΒξΙΚ¬ρΜ®Ζ―…ΌΘΜ
Θ§‘ρΥϊ‘ΎΦΉΓΔ““ΝΫΗω≈ζΖΔΒξ÷–ΒΡ___________≈ζΖΔΒξΙΚ¬ρΜ®Ζ―…ΌΘΜ
Δέ»τ–Γ’≈‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΜ®Ζ―ΝΥ460‘ΣΘ§‘ρΥϊ‘ΎΦΉΓΔ““ΝΫΗω≈ζΖΔΒξ÷–ΒΡ___________≈ζΖΔΒξΙΚ¬ρ ΐΝΩΕύΘ°
ΓΨ¥πΑΗΓΩΘ®1Θ©100Θ§750Θ§140Θ§700ΘΜΘ®2Θ©y1=5xΘ®xΘΨ0Θ©ΘΜ ![]() ΘΜΘ®3Θ©ΔΌ100ΘΜΔΎ““ΘΜΔέΦΉ
ΘΜΘ®3Θ©ΔΌ100ΘΜΔΎ““ΘΜΔέΦΉ
ΓΨΫβΈωΓΩ
Θ®1Θ©ΦΉ≈ζΖΔΒξΜ®Ζ―Ζ÷±π”Ο20ΚΆ150≥Υ“‘5Φ¥Ω…«σ≥ωΘΜ““≈ζΖΔΒξΒΡΜ®Ζ―Θ§ 20«ßΩΥ ±Θ§”Ο20ΓΝ7Θ§150«ßΩΥ ±Τδ÷–”–![]() ΒΡΦέΗώΈΣ6‘Σ/
ΒΡΦέΗώΈΣ6‘Σ/![]() Θ§≥§Ιΐ
Θ§≥§Ιΐ![]() ≤ΩΖ÷ΒΡΦέΗώΈΣ4‘Σ/
≤ΩΖ÷ΒΡΦέΗώΈΣ4‘Σ/![]() ΦΤΥψΦ¥Ω…«σ≥ω¥πΑΗΘΜ
ΦΤΥψΦ¥Ω…«σ≥ω¥πΑΗΘΜ
Θ®2Θ©ΗυΨίΝΫΗωΒξΒΡ”≈ΜίΖΫΑΗΘ§άϊ”ΟΉήΜ®Ζ―=“Μ¥Έ–‘ΙΚ¬ρΒΡ ΐΝΩΓΝΒΞΦέΦ¥Ω…ΒΟ≥ωΚ· ΐΙΊœΒ ΫΘΜ
Θ®3Θ©ΔΌΝνΘ®2Θ©÷–ΒΡ![]() «σ≥ωœύ”ΠΒΡx÷ΒΦ¥Ω…ΘΜ
«σ≥ωœύ”ΠΒΡx÷ΒΦ¥Ω…ΘΜ
ΔΎΫΪ![]() Ζ÷±π¥ζ»κ
Ζ÷±π¥ζ»κ![]() ÷–Θ§«σ≥ωœύ”ΠΒΡ
÷–Θ§«σ≥ωœύ”ΠΒΡ![]() Θ§»ΜΚσΫχ––±»ΫœΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
Θ§»ΜΚσΫχ––±»ΫœΦ¥Ω…ΒΟ≥ω¥πΑΗΘΜ
ΔέΝν![]() Θ§»ΜΚσΖ÷±π«σ≥ωœύ”ΠΒΡx÷ΒΘ§»ΜΚσΫχ––±»ΫœΦ¥Ω…Θ°
Θ§»ΜΚσΖ÷±π«σ≥ωœύ”ΠΒΡx÷ΒΘ§»ΜΚσΫχ––±»ΫœΦ¥Ω…Θ°
ΫβΘΚΘ®1Θ©ΦΉ≈ζΖΔΒξΘΚ![]() ‘ΣΘ§
‘ΣΘ§![]() ‘ΣΘΜ
‘ΣΘΜ
““≈ζΖΔΒξΘΚ![]() ‘ΣΘ§
‘ΣΘ§![]() ‘ΣΘ°
‘ΣΘ°
Ι “ά¥ΈΧν–¥ΘΚ100Θ§750Θ§140Θ§700ΘΜ
Θ®2Θ©ΗυΨίΧβ“β”–Θ§
y1=5xΘ®xΘΨ0Θ©
Β±0ΘΦxΓή50 ±Θ§y2=7xΘ®0ΘΦxΓή50Θ©
Β±xΘΨ50 ±Θ§y2=6ΓΝ50+4Θ®x-50Θ©=4x+100Θ®xΘΨ50Θ©
“ρ¥Υy1Θ§y2”κxΒΡΚ· ΐΫβΈω ΫΈΣΘΚ
y1=5xΘ®xΘΨ0Θ©Θ§![]() ΘΜ
ΘΜ
Θ®3Θ©ΔΌΒ±y1=y2 ±Θ§”–ΘΚ5x=7xΘ§ΫβΒΟx=0Θ§≤ΜΚœΧβ“βΘ§…α»ΞΘΜ
Β±y1=y2 ±Θ§“≤”–ΘΚ5x=4x+100Θ§ΫβΒΟx=100Θ§
ΓύΥϊ‘ΎΆ§“ΜΗω≈ζΖΔΒξ“Μ¥ΈΙΚ¬ρΤΜΙϊΒΡ ΐΝΩΈΣ100«ßΩΥΘ°
ΔΎΒ±x=120 ±Θ§y1=5ΓΝ120=600‘ΣΘ§y2=4ΓΝ120+100=580‘ΣΘ§
ΓΏ600ΘΨ580
Γύ““≈ζΖΔΒξΜ®Ζ―…ΌΘ°
ΔέΒ±![]() ±Θ§Φ¥ΘΚ5x=460ΚΆ4x+100=460Θ§ΫβΒΟx1=92ΚΆx2=90Θ§
±Θ§Φ¥ΘΚ5x=460ΚΆ4x+100=460Θ§ΫβΒΟx1=92ΚΆx2=90Θ§
ΓΏ92ΘΨ90
ΓύΦΉ≈ζΖΔΒξΙΚ¬ρ ΐΝΩΕύΘ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΉΓΔ““ΝΫΈΜ‘ΥΕ·‘±‘ΎœύΆ§ΧθΦΰœ¬Ης…δΜς![]() ¥ΈΘ§≥…Φ®»γœ¬: ΦΉ:
¥ΈΘ§≥…Φ®»γœ¬: ΦΉ:![]() ; ““:
; ““:![]() ΗυΨί…œ ω–≈œΔΘ§œ¬Ν–Ϋα¬έ¥μΈσΒΡ «Θ® Θ©
ΗυΨί…œ ω–≈œΔΘ§œ¬Ν–Ϋα¬έ¥μΈσΒΡ «Θ® Θ©
A.ΦΉΓΔ““ΒΡ÷Ύ ΐΖ÷±π «![]() B.ΦΉΓΔ““ΒΡ÷–ΈΜ ΐΖ÷±π «
B.ΦΉΓΔ““ΒΡ÷–ΈΜ ΐΖ÷±π «![]()
C.““ΒΡ≥…Φ®±»ΫœΈ»Ε®D.ΦΉΓΔ““ΒΡΤΫΨυ ΐΖ÷±π «![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
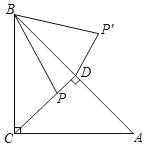
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ACΘΫBCΘΫ4Θ§P «ΓςABCΒΡΗΏCD…œ“ΜΗωΕ·ΒψΘ§“‘BΒψΈΣ–ΐΉΣ÷––ΡΑ―œΏΕΈBPΡφ ±’κ–ΐΉΣ45ΓψΒΟΒΫBPΓδΘ§Ν§Ϋ”DPΓδΘ§‘ρDPΓδΒΡΉν–Γ÷Β «Θ®ΓΓΓΓΘ©
A.2![]() -2B.4©¹2
-2B.4©¹2![]() C.2©¹
C.2©¹![]() D.
D.![]() -1
-1
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
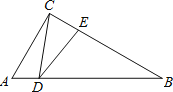
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœACBΘΫ90ΓψΘ§ΓœAΘΫ60ΓψΘ§ACΘΫ2Θ§D «AB±Ώ…œ“ΜΗωΕ·ΒψΘ®≤Μ”κΒψAΓΔB÷ΊΚœΘ©Θ§E «BC±Ώ…œ“ΜΒψΘ§«“ΓœCDEΘΫ30ΓψΘ°…ηADΘΫxΘ§BEΘΫyΘ§‘ρœ¬Ν–ΆΦœσ÷–Θ§Ρή±μ Ψy”κxΒΡΚ· ΐΙΊœΒΒΡΆΦœσ¥σ÷¬ «Θ®ΓΓΓΓΘ©
A.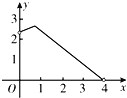 B.
B.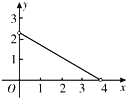 C.
C. D.
D.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
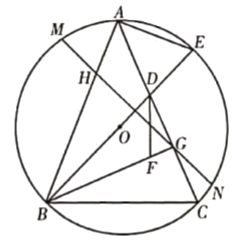
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§‘ΎΨΊ–ΈABCD÷–Θ§ΒψP «BC±Ώ…œ“ΜΒψΘ§Ν§Ϋ”APΫΜΕ‘Ϋ«œΏBD”ΎΒψE,![]() .ΉςœΏΕΈAPΒΡ÷–¥ΙœΏMNΖ÷±πΫΜœΏΕΈDC,DB,AP,AB”ΎΒψM,G,FΘ§N.
.ΉςœΏΕΈAPΒΡ÷–¥ΙœΏMNΖ÷±πΫΜœΏΕΈDC,DB,AP,AB”ΎΒψM,G,FΘ§N.
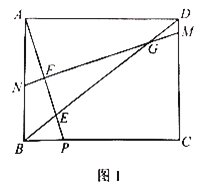
Θ®1Θ©«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() Θ§«σ
Θ§«σ![]() .
.
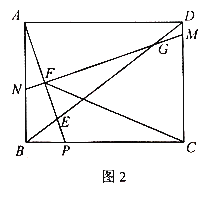
Θ®3Θ©»γΆΦ2Θ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§Ν§Ϋ”CFΘ§«σ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβΡ≥–Θ―ß…ζΕ‘ΓΕΉν«Ω¥σΡ‘ΓΖΓΔΓΕά ΕΝ’ΏΓΖΓΔΓΕ÷–Ιζ Ϊ¥ ¥σΜαΓΖΓΔΓΕ≥ω≤ ÷–Ιζ»ΥΓΖΥΡΗωΒγ ”ΫΎΡΩΒΡœ≤Α°«ιΩωΘ§Υφ•i≥ι»ΓΝΥ![]() Οϊ―ß…ζΫχ––Βς≤ιΆ≥ΦΤΘ®“Σ«σΟΩΟϊ―ß…ζ―Γ≥ω≤Δ«“÷ΜΡή―Γ≥ω“ΜΗωΉ‘ΦΚΉνœ≤Α°ΒΡΫΎΡΩΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γΆΦΆ≥ΦΤΆΦ±μΘΚ
Οϊ―ß…ζΫχ––Βς≤ιΆ≥ΦΤΘ®“Σ«σΟΩΟϊ―ß…ζ―Γ≥ω≤Δ«“÷ΜΡή―Γ≥ω“ΜΗωΉ‘ΦΚΉνœ≤Α°ΒΡΫΎΡΩΘ©Θ§≤ΔΫΪΒς≤ιΫαΙϊΜφ÷Τ≥…»γΆΦΆ≥ΦΤΆΦ±μΘΚ
―ß…ζΉνœ≤Α°ΒΡΫΎΡΩ»Υ ΐΆ≥ΦΤ±μ
ΫΎΡΩ | »Υ ΐΘ®ΟϊΘ© | ΑΌΖ÷±» |
Ήν«Ω¥σΡ‘ |
|
|
ά ΕΝ’Ώ |
|
|
÷–Ιζ Ϊ¥ ¥σΜα |
|
|
≥ω≤ ÷–Ιζ |
|
|

ΗυΨί“‘…œΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
Θ®1Θ©![]() ______Θ§
______Θ§![]() _____Θ§
_____Θ§![]() ____ΘΜ
____ΘΜ
Θ®2Θ©≤Ι»Ϊ…œΟφΒΡΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®3Θ©»τΗΟ–ΘΙ≤”–―ß…ζ5000ΟϊΘ§ΗυΨί≥ι―υΒς≤ιΫαΙϊΘ§ΙάΦΤΗΟ–ΘΉνœ≤Α°ΓΕ÷–Ιζ Ϊ¥ ¥σΜαΓΖΫΎΡΩΒΡ―ß…ζ”–Εύ…ΌΟϊΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
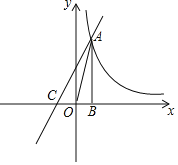
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΖ¥±»άΐΚ· ΐyΘΫ![]() ΒΡΆΦœσΨ≠ΙΐΒΎ“ΜœσœόΡΎΒΡ“ΜΒψA(nΘ§4)Θ§ΙΐΒψAΉςABΓΆx÷α”ΎΒψBΘ§«“ΓςAOBΒΡΟφΜΐΈΣ2Θ°
ΒΡΆΦœσΨ≠ΙΐΒΎ“ΜœσœόΡΎΒΡ“ΜΒψA(nΘ§4)Θ§ΙΐΒψAΉςABΓΆx÷α”ΎΒψBΘ§«“ΓςAOBΒΡΟφΜΐΈΣ2Θ°
(1)«σmΚΆnΒΡ÷ΒΘΜ
(2)»τ“Μ¥ΈΚ· ΐyΘΫkx+2ΒΡΆΦœσΨ≠ΙΐΒψAΘ§≤Δ«“”κx÷αœύΫΜ”ΎΒψCΘ§«σœΏΕΈACΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ ![]() «
«![]() ΒΡΝΫΧθœ“Θ§
ΒΡΝΫΧθœ“Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ§
Θ§![]() ΒΡΤΫΖ÷œΏΫΜ
ΒΡΤΫΖ÷œΏΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΜ
Θ§ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]()
![]() »γΆΦ1Θ§«σ
»γΆΦ1Θ§«σ![]() ΒΡΕ» ΐΘΜ
ΒΡΕ» ΐΘΜ

![]() »γΆΦ2Θ§
»γΆΦ2Θ§![]() ΈΣ
ΈΣ![]() …œ“ΜΒψΘ§Ν§Ϋ”
…œ“ΜΒψΘ§Ν§Ϋ”![]() Θ§Β±
Θ§Β±![]() ±Θ§«σ÷ΛΘΚ
±Θ§«σ÷ΛΘΚ![]()

![]() »γΆΦ3 Θ§‘Ύ
»γΆΦ3 Θ§‘Ύ![]() ΒΡΧθΦΰœ¬Θ§Β±
ΒΡΧθΦΰœ¬Θ§Β±![]() ΈΣ
ΈΣ![]() ΒΡ÷±ΨΕ ±Θ§Ψ≠ΙΐΒψ
ΒΡ÷±ΨΕ ±Θ§Ψ≠ΙΐΒψ![]() ΒΡœ“
ΒΡœ“![]() ΫΜ
ΫΜ![]() ”ΎΒψ
”ΎΒψ![]() Θ§»τ
Θ§»τ![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() Θ§«σœΏΕΈ
Θ§«σœΏΕΈ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
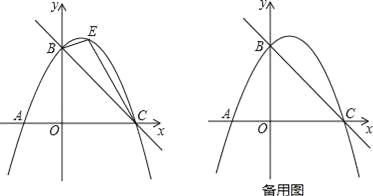
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏy=©¹![]() x+3”κx÷αΫΜ”ΎΒψCΘ§”κy÷αΫΜ”ΎΒψBΘ§≈ΉΈοœΏy=ax2+
x+3”κx÷αΫΜ”ΎΒψCΘ§”κy÷αΫΜ”ΎΒψBΘ§≈ΉΈοœΏy=ax2+![]() x+cΨ≠ΙΐBΓΔCΝΫΒψΘ°
x+cΨ≠ΙΐBΓΔCΝΫΒψΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦΘ§ΒψE «÷±œΏBC…œΖΫ≈ΉΈοœΏ…œΒΡ“ΜΕ·ΒψΘ§Β±ΓςBECΟφΜΐΉν¥σ ±Θ§«κ«σ≥ωΒψEΒΡΉχ±ξΚΆΓςBECΟφΜΐΒΡΉν¥σ÷ΒΘΩ
Θ®3Θ©‘ΎΘ®2Θ©ΒΡΫα¬έœ¬Θ§ΙΐΒψEΉςy÷αΒΡΤΫ––œΏΫΜ÷±œΏBC”ΎΒψMΘ§Ν§Ϋ”AMΘ§ΒψQ «≈ΉΈοœΏΕ‘≥Τ÷α…œΒΡΕ·ΒψΘ§‘Ύ≈ΉΈοœΏ…œ «Ζώ¥φ‘ΎΒψPΘ§ ΙΒΟ“‘PΓΔQΓΔAΓΔMΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘΩ»γΙϊ¥φ‘ΎΘ§«κ÷±Ϋ”–¥≥ωΒψPΒΡΉχ±ξΘΜ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com