
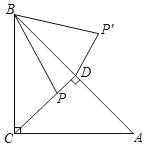
【题目】如图,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一个动点,以B点为旋转中心把线段BP逆时针旋转45°得到BP′,连接DP′,则DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
【答案】A
【解析】
在BC上截取BE=BD,根据等腰直角三角形的性质求得BA和BE,再由旋转的性质证明△BDP'≌△BEP,从而可得到PE=P'D,再由等腰直角三角形的性质求得PE,从而求得DP′的最小值.
解:如图,在BC上截取BE=BD,
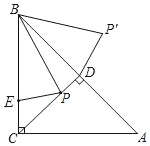
∵∠ACB=90°,AC=BC=4, CD⊥AB,
∴BA=4![]() ,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2
,∠ABC=∠BAC=∠BCD=∠DCA=45°,BD=CD=AD=2![]() =BE,
=BE,
∵旋转
∴BP=BP',∠PBP'=45°,
∵BE=BD,∠ABC=∠PBP'=45°,BP=BP'
∴△BDP'≌△BEP(SAS)
∴PE=P'D
∴当PE⊥CD时,PE有最小值,即DP'有最小值,
∵PE⊥CD,∠BCD=45°,
∴CE=![]() PE=BC﹣BE=4﹣2
PE=BC﹣BE=4﹣2![]()
∴P'D =PE=2![]() ﹣2
﹣2
故选:A.


科目:初中数学 来源: 题型:
【题目】在△ABC中,内角A、B、C的对边分别为a、b、c.若b2+c2=2b+4c﹣5且a2=b2+c2﹣bc,则△ABC的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国魏晋时期的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示,若a=2,b=3,现随机向该图形内掷一枚小针,则针尖落在阴影域内的概率为_____.
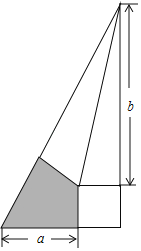
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
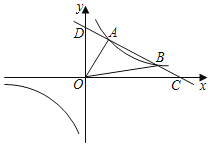
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
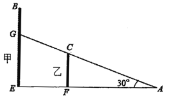
【题目】如图,某汽车司机在平坦的公路上行驶,前面出现两个建筑物,在A处司机能看到甲建筑物一部分(把汽车看成一个点),这时视线与公路夹角为30°;
(1)汽车行驶到什么位置时,司机刚好看不到甲建筑物?请在图中标出这个D点;
(2)若CF的高度40米,当刚好看不到甲建筑物时,司机的视线与与公路夹角为45°,请问汽车行驶了多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校3月份开展网络授课教学,该校随机抽取部分学生,按四个类别(A、很喜欢;B、喜欢;C、一般;D、不喜欢;)统计它们对网络授课的接受情况,并将结果绘制成如下两幅不完整的统计图:
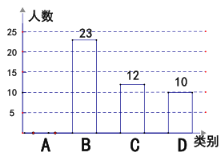
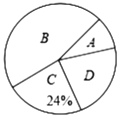
(1)这次共抽取_________名学生进行统计调查;扇形统计图中,D类所对应的扇形圆心角的大小为_______;
(2)将条形图补充完整;
(3)该校共有1500名学生,估计该校表示“喜欢”网络授课的B类的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个批发店销售同一种苹果,在甲批发店,不论一次购买数量是多少,价格均为5元/![]() .在乙批发店,一次购买数量不超过
.在乙批发店,一次购买数量不超过![]() 时,价格为7元/
时,价格为7元/![]() ;一次购买数量超过
;一次购买数量超过![]() 时,其中有
时,其中有![]() 的价格为6元/
的价格为6元/![]() ,超过
,超过![]() 部分的价格为4元/
部分的价格为4元/![]() .设小张在同一个批发店一次购买苹果的数量为
.设小张在同一个批发店一次购买苹果的数量为![]() .
.
(1)根据题意填表:
一次购买数量/ | 20 | 50 | 150 | … |
甲批发店花费/元 | 250 | … | ||
乙批发店花费/元 | 350 | … |
(2)设在甲批发店花费![]() 元,在乙批发店花费
元,在乙批发店花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若小张在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为_________![]() ;
;
②若小张在同一个批发店一次购买苹果的数量为![]() ,则他在甲、乙两个批发店中的___________批发店购买花费少;
,则他在甲、乙两个批发店中的___________批发店购买花费少;
③若小张在同一个批发店一次购买苹果花费了460元,则他在甲、乙两个批发店中的___________批发店购买数量多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据2019年莆田市初中毕业升学体育考试内容要求,甲、乙、丙在某节体育课他们各自随机分别到篮球场A处进行篮球运球绕杆往返训练或到足球场B处进行足球运球绕杆训练,三名学生随机选择其中的一场地进行训练.
(1)用列表法或树形图表示出的所用可能出现的结果;
(2)求甲、乙、丙三名学生在同一场地进行训练的概率;
(3)求甲、乙、丙三名学生中至少有两人在B处场地进行训练的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com