
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴相交于负半轴,给出五个结论:①a+b+c=0,②abc<0,③2a+b>0,④a+c=1,⑤当﹣1<x<1时,y<0;其中正确的结论的序号( )
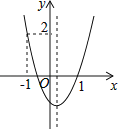
A.①③⑤B.②③④C.①③④D.②③⑤
【答案】C
【解析】
①中,抛物线点(1,0),代入可得结论;
②中,抛物线开口可判断a的符号,对称轴的位置可判断b的符号,抛物线与y轴的交点可判断c的符号;
③中,利用对称轴小于1可判断2a+b的符号;
④中,将点(﹣1,2)和(1,0)代入函数,可得a+c的值;
⑤中,根据抛物线与x轴的另一个交点在(﹣1,0)和(0,0)之间可判断y的取值范围.
解:∵抛物线经过点(1,0),即x=1时,y=0,
∴a+b+c=0,所以①正确;
∵抛物线开口向上,
∴a>0,
∵抛物线的对称轴在y轴的右侧,
∴a、b异号,即b<0,
∵抛物线与y轴相交于负半轴,
∴c<0,
∴abc>0,所以②错误;
∵x=![]() <1,
<1,
而a>0,
∴﹣b<2a,
即2a+b>0,所以③正确;
∵二次函数经过点(﹣1,2)和(1,0),
∴a﹣b+c=2,a+b+c=0,
∴2a+2c=2,即a+c=1,所以④正确;
∵抛物线与x轴的另一个交点在(﹣1,0)和(0,0)之间,
∴当﹣1<x<0时,y不一定小于0,所以⑤错误.
故选:C.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案科目:初中数学 来源: 题型:
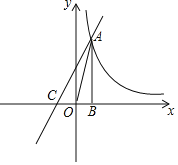
【题目】如图,已知反比例函数y=![]() 的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
的图象经过第一象限内的一点A(n,4),过点A作AB⊥x轴于点B,且△AOB的面积为2.
(1)求m和n的值;
(2)若一次函数y=kx+2的图象经过点A,并且与x轴相交于点C,求线段AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
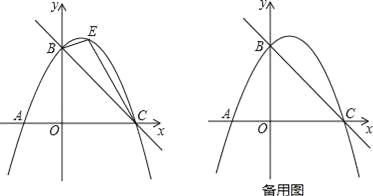
【题目】如图,直线y=﹣![]() x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+![]() x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
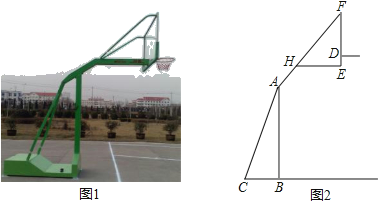
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
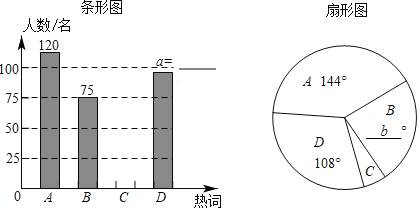
【题目】网络时代,新兴词汇层出不穷.为了解大众对网络词汇的理解,某兴趣小组举行了一个“我是路人甲”的调查活动:选取四个热词A:“硬核人生”,B:“好嗨哦”,C:“双击666”,D:“杠精时代”在街道上对流动人群进行了抽样调查,要求被调查的每位只能勾选一个最熟悉的热词,根据调查结果,该小组绘制了如下的两幅不完整的统计图,请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名路人.
(2)补全条形统计图;
(3)扇形图中的b= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期,大兴区开展了“恰同学少年,品诗词美韵”中华传统诗词大赛活动![]() 小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
小江统计了班级30名同学四月份的诗词背诵数量,具体数据如表所示:
诗词数量 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
人数 | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
那么这30名同学四月份诗词背诵数量的众数和中位数分别是![]()
![]()
A. 11,7 B. 7,5 C. 8,8 D. 8,7
查看答案和解析>>
科目:初中数学 来源: 题型:
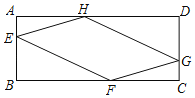
【题目】如图,点E、F、G、H分别在矩形ABCD的边AB、BC、CD、DA(不包括端点)上运动,且满足![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)试判断四边形EFGH的形状,并说明理由.
(3)请探究四边形EFGH的周长一半与矩形ABCD一条对角线长的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
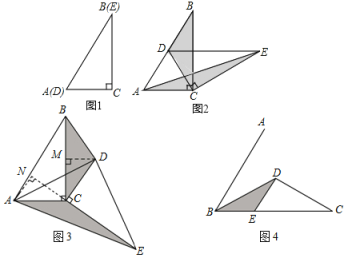
【题目】如图1,将两个完全相同的三角形纸片![]() 和
和![]() 重合放置,其中
重合放置,其中![]() ,
,![]() .
.
(1)操作发现
如图2,固定![]() ,使
,使![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 恰好落在
恰好落在![]() 边上时,填空:
边上时,填空:
①线段![]() 与
与![]() 的位置关系是______;
的位置关系是______;
②设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,则
,则![]() 与
与![]() 的数量关系是______
的数量关系是______
(2)猜想论证
当![]() 绕点
绕点![]() 旋转到如图3所示的位置时,小明猜想1.中
旋转到如图3所示的位置时,小明猜想1.中![]() 与
与![]() 的数量关系仍然成立,并尝试分别作出了
的数量关系仍然成立,并尝试分别作出了![]() 和
和![]() 中
中![]() 、
、![]() 边上的高,请你证明小明的猜想.
边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点![]() 是角平分线上一点,
是角平分线上一点,![]() ,
,![]() 交
交![]() 于点
于点![]() (如图4).若在射线
(如图4).若在射线![]() 上存在点
上存在点![]() ,使
,使![]() ,请求出相应的
,请求出相应的![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com