
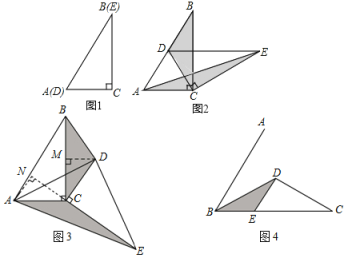
ЁОЬтФПЁПШчЭМ1ЃЌНЋСНИіЭъШЋЯрЭЌЕФШ§НЧаЮжНЦЌ![]() КЭ
КЭ![]() жиКЯЗХжУЃЌЦфжа
жиКЯЗХжУЃЌЦфжа![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉВйзїЗЂЯж
ШчЭМ2ЃЌЙЬЖЈ![]() ЃЌЪЙ
ЃЌЪЙ![]() ШЦЕу
ШЦЕу![]() а§зЊЃЌЕБЕу
а§зЊЃЌЕБЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() БпЩЯЪБЃЌЬюПеЃК
БпЩЯЪБЃЌЬюПеЃК
ЂйЯпЖЮ![]() гы
гы![]() ЕФЮЛжУЙиЯЕЪЧ______ЃЛ
ЕФЮЛжУЙиЯЕЪЧ______ЃЛ
ЂкЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЪЧ______
ЕФЪ§СПЙиЯЕЪЧ______
ЃЈ2ЃЉВТЯыТлжЄ
ЕБ![]() ШЦЕу
ШЦЕу![]() а§зЊЕНШчЭМ3ЫљЪОЕФЮЛжУЪБЃЌаЁУїВТЯы1ЃЎжа
а§зЊЕНШчЭМ3ЫљЪОЕФЮЛжУЪБЃЌаЁУїВТЯы1ЃЎжа![]() гы
гы![]() ЕФЪ§СПЙиЯЕШдШЛГЩСЂЃЌВЂГЂЪдЗжБ№зїГіСЫ
ЕФЪ§СПЙиЯЕШдШЛГЩСЂЃЌВЂГЂЪдЗжБ№зїГіСЫ![]() КЭ
КЭ![]() жа
жа![]() ЁЂ
ЁЂ![]() БпЩЯЕФИпЃЌЧыФужЄУїаЁУїЕФВТЯыЃЎ
БпЩЯЕФИпЃЌЧыФужЄУїаЁУїЕФВТЯыЃЎ
ЃЈ3ЃЉЭиеЙЬНОП
вбжЊЁЯABC=60ЁуЃЌЕу![]() ЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌ
ЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() (ШчЭМ4)ЃЎШєдкЩфЯп
(ШчЭМ4)ЃЎШєдкЩфЯп![]() ЩЯДцдкЕу
ЩЯДцдкЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌЧыЧѓГіЯргІЕФ
ЃЌЧыЧѓГіЯргІЕФ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉВйзїЗЂЯжЃКЂйDEЁЮACЃЛЂк![]() =
=![]() ЃЛЃЈ2ЃЉВТЯыТлжЄЃК
ЃЛЃЈ2ЃЉВТЯыТлжЄЃК![]() =
=![]() ШдШЛГЩСЂЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЭиеЙЬНОПЃК
ШдШЛГЩСЂЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЭиеЙЬНОПЃК![]() =
=![]() Лђ
Лђ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉВйзїЗЂЯжЃКЂйИљОнжБНЧШ§НЧаЮЕФаджЪМДПЩЧѓГіЁЯEDCЃЌШЛКѓжЄГіЁїCADЮЊЕШБпШ§НЧаЮПЩЕУЁЯDCA=60ЁуЃЌДгЖјЕУГіЁЯEDC=ЁЯDCAЃЌШЛКѓИљОнЦНааЯпЕФХаЖЈМДПЩЕУГіНсТлЃЛ
ЂкИљОнЦНааЯпжЎМфЕФОрРыДІДІЯрЕШКЭЭЌЕзЕШИпПЩЕУSЁїDAC=![]() ЃЌШЛКѓИљОн30ЁуЫљЖдЕФжБНЧБпЪЧаББпЕФвЛАыКЭЕШБпШ§НЧаЮЕФаджЪПЩЕУЕуDЮЊABЕФжаЕуЃЌДгЖјжЄГіSЁїDAC=
ЃЌШЛКѓИљОн30ЁуЫљЖдЕФжБНЧБпЪЧаББпЕФвЛАыКЭЕШБпШ§НЧаЮЕФаджЪПЩЕУЕуDЮЊABЕФжаЕуЃЌДгЖјжЄГіSЁїDAC=![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉВТЯыТлжЄЃКРћгУAASжЄГіЁїACNЁеЁїDCMЃЌМДПЩЕУГіAN=DMЃЌШЛКѓИљОна§зЊЕФаджЪПЩЕУEC=BCЃЌШЛКѓИљОнСНИіШ§НЧаЮЕШЕзЕШИпМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЭиеЙЬНОПЃКбгГЄCDНЛABгкЕуHЃЌЙ§ЕуEзїEGЁЭBDгкGЃЌРћгУ30ЁуЫљЖдЕФжБНЧБпЪЧаББпЕФвЛАыКЭЙДЙЩЖЈРэЗжБ№ЧѓГіBHКЭGEЃЌШЛКѓИљОнЕуFЕФЮЛжУЗжРрЬжТлЃЌИљОнСНИіШ§НЧаЮЕФУцЛ§ЯрЕШЁЂЕзЯрЕШФЧУДИпвВЯрЕШМДПЩЧѓГіFHЃЌДгЖјЗжБ№ЧѓГіBFЕФГЄ
НтЃКЃЈ1ЃЉВйзїЗЂЯжЃКЂйDEЁЮACЃЌРэгЩШчЯТЃК
Ёп![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЁрЁЯBAC=90ЁуЃЁЯB=60ЁуЃЌЁЯEDC=90ЁуЃЁЯDEC=60Ёу
ЁпЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() БпЩЯЪБЃЌ
БпЩЯЪБЃЌ
ЁрCA=CD
ЁрЁїCADЮЊЕШБпШ§НЧаЮ
ЁрЁЯDCA=60Ёу
ЁрЁЯEDC=ЁЯDCA
ЁрDEЁЮAC
ЙЪД№АИЮЊЃКDEЁЮACЃЎ
Ђк![]() =
=![]() ЃЌРэгЩШчЯТ
ЃЌРэгЩШчЯТ
ЁпDEЁЮAC
ИљОнЦНааЯпжЎМфЕФОрРыДІДІЯрЕШ
ЁрSЁїDAC=![]()
дкRtЁїABCжаЃЌЁЯB=30Ёу
ЁрAB=2AC
ЁпЁїCADЮЊЕШБпШ§НЧаЮ
ЁрAC=AD
ЁрAB=2AD
ЁрЕуDЮЊABЕФжаЕу
ЁрSЁїDAC=![]()
Ёр![]() =
=![]()
ЙЪД№АИЮЊЃК![]() =
=![]() ЃЎ
ЃЎ
ЃЈ2ЃЉВТЯыТлжЄЃК![]() =
=![]() ШдШЛГЩСЂЃЌжЄУїШчЯТ
ШдШЛГЩСЂЃЌжЄУїШчЯТ
ЁпANЁЂDMЗжБ№ЪЧЁїACEЁЂЁїBCDБпЩЯЕФИп
ЁрЁЯANC=ЁЯDMC=90Ёу
ЁпЁЯACNЃЋЁЯNCB=90ЁуЃЌЁЯDCMЃЋЁЯNCB=90Ёу
ЁрЁЯACN=ЁЯDCM
дкЁїACNКЭЁїDCMжа
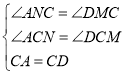
ЁрЁїACNЁеЁїDCM
ЁрAN=DM
ЁпEC=BC
ЁрЁїACEКЭЁїBCDЕШЕзЕШИп
Ёр![]() =
=![]()
ЃЈ3ЃЉЭиеЙЬНОПЃКбгГЄCDНЛABгкЕуHЃЌЙ§ЕуEзїEGЁЭBDгкGЃЌ
ЁпЁЯABC=60ЁуЃЌЕу![]() ЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌ
ЪЧНЧЦНЗжЯпЩЯвЛЕуЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯHBD=ЁЯCBD=![]() ЁЯABC=30Ёу
ЁЯABC=30Ёу
Ёп![]()
ЁрЁЯDCB=ЁЯDBC=30Ёу
ЁрЁЯBHC=180ЁуЃЁЯHBCЃЁЯDCB=90Ёу
дкRtЁїBDHжаЃЌHD=![]() ЃЌBH=
ЃЌBH=![]()
Ёп![]()
ЁрЁЯEDB=ЁЯHBD=30Ёу
ЁрЁЯEBD=ЁЯEDB
ЁрEB=ED
ЁрBG=![]() =2
=2
дкRtЁїBEGжаЃЌЩшGE=xЃЌBE=2GE=2x
ИљОнЙДЙЩЖЈРэПЩЕУЃКGE2ЃЋBG2=BE2
МДx 2ЃЋ22=ЃЈ2xЃЉ2
НтЕУЃКx=![]()
ЁрGE=![]()
ЃЈiЃЉЕБЕуFдкЯпЖЮBHЩЯЪБЃЌ
Ёп![]() ЃЌ
ЃЌ![]()
ЁрFH=GE=![]()
ЁрBF=BHЃFH=![]() ЃЛ
ЃЛ
ЃЈiiЃЉЕБ![]() дкЯпЖЮBHЕФбгГЄЯпЩЯЪБ
дкЯпЖЮBHЕФбгГЄЯпЩЯЪБ
ЭЌРэПЩЕУ![]() H= GE=
H= GE=![]()
ЁрB![]() =BHЃЋ
=BHЃЋ![]() H=
H=![]()
злЩЯЫљЪіЃК![]() =
=![]() Лђ
Лђ![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓПЊПкЯђЩЯЃЌЭМЯѓОЙ§Еу(Љ1ЃЌ2)КЭ(1ЃЌ0)ЃЌЧвгыyжсЯрНЛгкИКАыжсЃЌИјГіЮхИіНсТлЃКЂйa+b+c=0ЃЌЂкabcЃМ0ЃЌЂл2a+bЃО0ЃЌЂмa+c=1ЃЌЂнЕБЉ1ЃМxЃМ1ЪБЃЌyЃМ0ЃЛЦфжае§ШЗЕФНсТлЕФађКХ(ЁЁЁЁ)
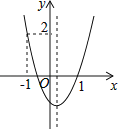
A.ЂйЂлЂнB.ЂкЂлЂмC.ЂйЂлЂмD.ЂкЂлЂн
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкABCDжаЃЌAEЁЭBCЃЌCFЁЭADЃЌEЃЌFЗжБ№ЮЊДЙзуЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїCDFЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮAECFЪЧОиаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌADЮЊBCБпЩЯЕФжаЯпЃЌEЮЊADЩЯвЛЖЏЕуЃЌЩшDEЃНnEAЃЌСЌНгCEВЂбгГЄЃЌНЛABгкЕуFЃЎ
ЃЈ1ЃЉГЂЪдЬНОПЃКШчЭМ1ЃЌЕБЁЯBACЃН90ЁуЃЌЁЯBЃН30ЁуЃЌDEЃНEAЪБЃЌBFЃЌBAжЎМфЕФЪ§СПЙиЯЕЪЧЁЁ ЁЁЃЛ
ЃЈ2ЃЉРрБШбгЩьЃКШчЭМ2ЃЌЕБЁїABCЮЊШёНЧШ§НЧаЮЃЌDEЃНEAЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыИјгшжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙЧЈвЦЃКШчЭМ3ЃЌЕБЁїABCЮЊШёНЧШ§НЧаЮЃЌDEЃНnEAЪБЃЌЧыжБНгаДГіBFЃЌBAжЎМфЕФЪ§СПЙиЯЕЃЎ
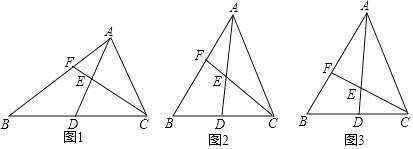
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжабЇзМБИОйАьвЛДЮбнНВБШШќЃЌУПАрЯоЖЈСНШЫБЈУћЃЌГѕШ§ЃЈ1ЃЉАрЕФШ§ЮЛЭЌбЇЃЈСНЮЛХЎЩњЃЌвЛЮЛФаЩњЃЉЖМЯыБЈУћВЮМгЃЌАржїШЮРюРЯЪІЩшМЦСЫвЛИіУўЧђгЮЯЗЃЌРћгУвббЇЙ§ЕФИХТЪжЊЪЖРДОіЖЈЫШЅВЮМгБШШќЃЌгЮЯЗЙцдђШчЯТЃКдквЛИіВЛЭИУїЕФЯфзгРяЗХ3ИіДѓаЁжЪЕиЭъШЋЯрЭЌЕФЦЙХвЧђЃЌдкет3ИіЦЙХвЧђЩЯЗжБ№аДЩЯ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЈУПИізжФИЗжБ№ДњБэвЛЮЛЭЌбЇЃЌЦфжа
ЃЈУПИізжФИЗжБ№ДњБэвЛЮЛЭЌбЇЃЌЦфжа![]() ЁЂ
ЁЂ![]() ЗжБ№ДњБэСНЮЛХЎЩњЃЌ
ЗжБ№ДњБэСНЮЛХЎЩњЃЌ![]() ДњБэФаЩњЃЉЃЌНСдШКѓЃЌРюРЯЪІДгЯфзгРяЫцЛњУўГівЛИіЦЙХвЧђЃЌВЛЗХЛиЃЌдйДЮНСдШКѓЫцЛњУўГіЕкЖўИіЦЙХвЧђЃЌИљОнЦЙХвЧђЩЯЕФзжФИОіЖЈЫШЅВЮМгБШШќЁЃ
ДњБэФаЩњЃЉЃЌНСдШКѓЃЌРюРЯЪІДгЯфзгРяЫцЛњУўГівЛИіЦЙХвЧђЃЌВЛЗХЛиЃЌдйДЮНСдШКѓЫцЛњУўГіЕкЖўИіЦЙХвЧђЃЌИљОнЦЙХвЧђЩЯЕФзжФИОіЖЈЫШЅВЮМгБШШќЁЃ
ЃЈ1ЃЉЧѓРюРЯЪІЕквЛДЮУўГіЕФЦЙХвЧђДњБэФаЩњЕФИХТЪЃЛ
ЃЈ2ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈЧѓЧЁКУбЁЖЈвЛУћФаЩњКЭвЛУћХЎЩњВЮШќЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁАаЃдААВШЋЁБЪмЕНШЋЩчЛсЕФЙуЗКЙизЂЃЌФГжабЇЖдВПЗжбЇЩњОЭаЃдААВШЋжЊЪЖЕФСЫНтГЬЖШЃЌВЩгУЫцЛњГщбљЕїВщЕФЗНЪНЃЌВЂИљОнЪеМЏЕНЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЌЧыИљОнЭГМЦЭМжаЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
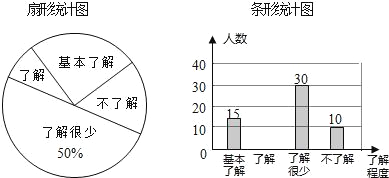
ЃЈ1ЃЉНгЪмЮЪОэЕїВщЕФбЇЩњЙВгаЁЁ ЁЁШЫЃЌЩШаЮЭГМЦЭМжаЁАЛљБОСЫНтЁБВПЗжЫљЖдгІЩШаЮЕФдВаФНЧЮЊЁЁ ЁЁЖШЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУжабЇЙВгабЇЩњ900ШЫЃЌЧыИљОнЩЯЪіЕїВщНсЙћЃЌЙРМЦИУжабЇбЇЩњжаЖдаЃдААВШЋжЊЪЖДяЕНЁАСЫНтЁБКЭЁАЛљБОСЫНтЁБГЬЖШЕФзмШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЭтНгдВЃЌ
ЕФЭтНгдВЃЌ![]() ЪЧжБОЖЃЌ
ЪЧжБОЖЃЌ![]() ЪЧ
ЪЧ![]() ЭтвЛЕуЧвТњзу
ЭтвЛЕуЧвТњзу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
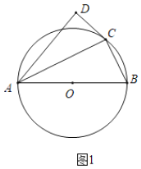
ЃЈ1ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЧаЯпЃЛ
ЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЛ
ЕФГЄЃЛ
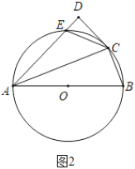
ЃЈ3ЃЉШчЭМ2ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() НЛгк
НЛгк![]() ЕуЃЌЪдаДГі
ЕуЃЌЪдаДГі![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() жЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
жЎМфЕФЪ§СПЙиЯЕВЂжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЁїABCКЭЁїCDEЖМЪЧЕШбќШ§НЧаЮЃЌЁЯBACЃНЁЯEDCЃН120ЁуЃЎ
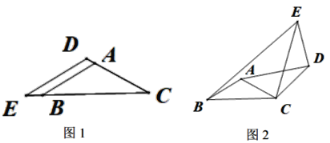
ЃЈ1ЃЉШчЭМ1ЃЌAЁЂDЁЂCдкЭЌвЛжБЯпЩЯЪБЃЌ![]() ЃН_______ЃЌ
ЃН_______ЃЌ![]() ЃН_______ЃЛ
ЃН_______ЃЛ
ЃЈ2ЃЉдкЭМ1ЕФЛљДЁЩЯЃЌЙЬЖЈЁїABCЃЌНЋЁїCDEШЦCа§зЊвЛЖЈЕФНЧЖШІС(0ЁуЃМІСЃМ360Ёу)ЃЌШчЭМ2ЃЌСЌНгADЁЂBEЃЎ
Ђй ![]() ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЕФжЕгаУЛгаИФБфЃПЧыЫЕУїРэгЩЃЎ
ЂкЭиеЙбаОПЃКШєABЃН1ЃЌDEЃН![]() ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ЃЌЕБ BЁЂDЁЂEдкЭЌвЛжБЯпЩЯЪБЃЌЧыМЦЫуЯпЖЮADЕФГЄЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКдкЁїABCжаЃЌABЃНACЃЌЕуDЪЧABЩЯвЛЕуЃЌвдBDЮЊжБОЖЕФЁб0гыACБпЯрЧагкЕуEЃЌНЛBCгкЕуFЃЌFGЁЭACгкЕуGЃЎ
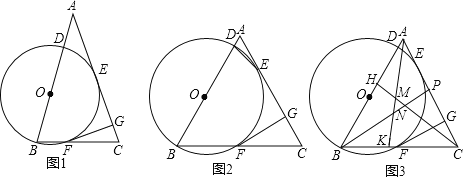
ЃЈ1ЃЉШчЭМlЃЌЧѓжЄЃКGEЃНGFЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгDEЃЌЁЯGFCЃН2ЁЯAEDЃЌЧѓжЄЃКЁїABCЮЊЕШБпШ§НЧаЮЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЕуHЁЂKЁЂPЗжБ№дкABЁЂBCЁЂACЩЯЃЌAKЁЂBPЗжБ№НЛCHгкЕуMЁЂNЃЌAHЃНBKЃЌЁЯPNCЉ![]() ЁЯBAKЃН60ЁуЃЌCNЃН6ЃЌCMЃН4
ЁЯBAKЃН60ЁуЃЌCNЃН6ЃЌCMЃН4![]() ЃЌЧѓBCЕФГЄЃЎ
ЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com