
����Ŀ������ij����ʵʩ��ҵ����ƶ������ƶ�����а�������Ķ������ֲ��Ʒ��ݮ����֪�ò�ݮ�ijɱ�Ϊÿǧ��10Ԫ����ݮ�����Ͷ���г����ۣ����г����鷢�֣���ݮ���۲����������ÿ���������y��ǧ�ˣ������۵���x��Ԫ/ǧ�ˣ�֮�亯����ϵ��ͼ��ʾ��

��1����y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��2������Ʒ�ֲ�ݮ�Ķ���Ϊ����ʱ��ÿ�����ۻ�����������������Ƕ��٣�
��3��ij������ݮ��ժ����30�죬Ԥ�Ʋ���6000ǧ�ˣ����գ�2���еķ�ʽ�������ۣ��ܷ�������������ݮ����˵�����ɣ�
���𰸡���1��y=-25x+700��10��x��28������2����Ʒ�ֲ�ݮ����Ϊ19Ԫ/ǧ��ʱ��ÿ�����ۻ�õ��������Ϊ2025Ԫ����3����������������ݮ�����ɼ�������
��������
��1�����ô���ϵ�������ɵý��ۣ�
��2�����ݡ�������=������������������г���������ʽ�����䷽�ɶ���ʽ���ɵó����ֵ��
��3������ڣ�2��������£���x=19ʱÿ������������ݴ����30��������������Ƚϼ��ɵó��𰸣�
��1����y��x�ĺ�����ϵʽΪy=kx+b��k��0������A��12��400����B��14��350���ֱ�����![]() ����ã�
����ã�![]() ����y��x�ĺ�����ϵʽΪy=-25x+700��������֪��
����y��x�ĺ�����ϵʽΪy=-25x+700��������֪��![]() ����10��x��28��
����10��x��28��
��2����ÿ�����������ΪwԪ��������֪w=��x-10����-25x+700��=-25x2+950x-7000 =-25��x-19��2+2025��
��a=-25��0���൱x=19ʱ��wȡ���ֵ��Ϊ2025��
����Ʒ�ֲ�ݮ����Ϊ19Ԫ/ǧ��ʱ��ÿ�����ۻ�õ��������Ϊ2025Ԫ��
��3����������������ݮ���������£�
��x=19ʱ��y=-25��19+700=225��225��30=6750��6000��
�ఴ�գ�2���еķ�ʽ�������ۣ��������꣮


 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ACB��90�㣬AC��BC������AB���е�OΪ����ԭ�㣬AB����ֱ��Ϊx�Ὠ����ƽ��ֱ������ϵ�У�����ABC�Ƶ�B˳ʱ����ת��ʹ��A��ת��y����������ϵĵ�A�䴦����AO��OB��2������Ӱ�������Ϊ��������
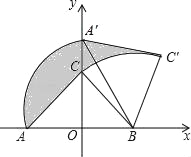
A. ��B. ![]() ����1C.
����1C. ![]() +1D.
+1D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ����̽��
����̽��
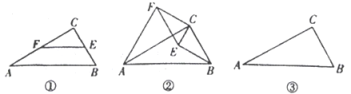
��ͼ-![]() ���ڡ�ABC�У���C=90�㣬��A=30�㣬��E��F�ֱ���BC��AC���ϵĵ㣬��EF//BC.
���ڡ�ABC�У���C=90�㣬��A=30�㣬��E��F�ֱ���BC��AC���ϵĵ㣬��EF//BC.
![]()
![]() ��ֵΪ ��
��ֵΪ ��![]() ֱ��
ֱ��![]() ��ֱ��
��ֱ��![]() ��λ�ù�ϵΪ ��
��λ�ù�ϵΪ ��
![]() �������
�������
��ͼ![]() ������ͼ
������ͼ![]() �е�
�е�![]() �Ƶ�
�Ƶ�![]() ˳ʱ����ת������
˳ʱ����ת������![]() ��������ת�Ĺ����У����ж�
��������ת�Ĺ����У����ж�![]() ��ֵ��ֱ��
��ֵ��ֱ��![]() ��ֱ
��ֱ![]() �ߵ�λ�ù�ϵ����˵�����ɣ�
�ߵ�λ�ù�ϵ����˵�����ɣ�
![]() ��չ����
��չ����
��![]() ������ת�����У���
������ת�����У���![]() ������ͬһֱ����ʱ����ֱ��д����ʱ�߶�
������ͬһֱ����ʱ����ֱ��д����ʱ�߶�![]() �ij�.
�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB = 90����BC = 3��AC = 4����DΪ��AB��һ�㣮����BCD��ֱ��CD���ۣ���B���ڵ�E��������AE�����AE // CD����ôBE =________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
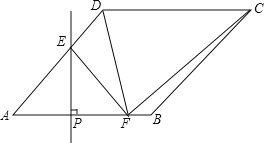
����Ŀ����ͼ��������ABCD�У���DAB=45�㣬AB=4����PΪ�߶�AB��һ���㣬����P��PE��AB��ֱ��AD�ڵ�E������A��PE�۵�����A����F��������DF��CF������CDFΪֱ��������ʱ���߶�AP�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
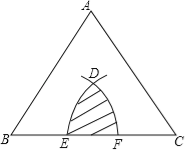
����Ŀ����ͼ����������ABC�ı߳���2���ֱ��Ե�B��CΪԲ�ģ���rΪ�뾶�������������������BCΧ�ɵ���Ӱ�������ΪS����![]() ��r��2ʱ��S��ȡֵ��Χ���� ����
��r��2ʱ��S��ȡֵ��Χ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
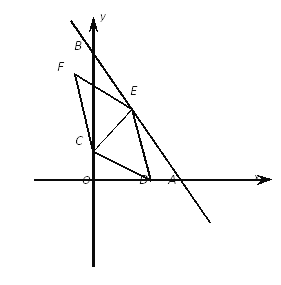
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��x�ᣬy��ֱ���A��12��0����B��0��16������C��B�������y�Ḻ������ÿ��2����λ���ٶ��˶�������C��CE��AB�ڵ�E����DΪx����һ���㣬����CD��DE����CD��DEΪ������CDEF.���˶�ʱ��Ϊt��.
��1�����C�˶��˶�����.ʱ����Eǡ����AB���е㣿
��2����t=4ʱ������CDEF�Ķ���Fǡ������y���ϣ��������ʱ��D�����ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
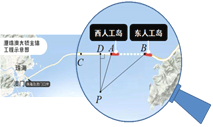
����Ŀ��2018��10��23�գ�����Ĵ�����ʽ��ͨ����Ϊ��ب���������ϵ�һ�������ķ羰.�������幤�������Ķ��������˸�������һ�������˹��������ν������ͺ������������˹����ϵ�A��Ͷ��˹����ϵ�B���ľ���ԼΪ5.6ǧ�ף���C�������˹��������Ĵ����ϵ�һ�㣬A��B��C��һ��ֱ���ϣ���ͼ��һ�ҹ۹�������![]() �δ�ֱ�ķ����У�����P��ʱ�۲������˹������ֱ���
�δ�ֱ�ķ����У�����P��ʱ�۲������˹������ֱ���![]() ��۹����
��۹����![]() �ļнǡ�DPA=18�㣬��DPB=53�㣬���ʱ�۹������AC�εľ���
�ļнǡ�DPA=18�㣬��DPB=53�㣬���ʱ�۹������AC�εľ���![]() �ij���
�ij���
�ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
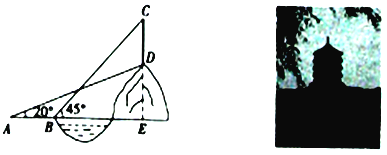
����Ŀ��������λ�ں���ʡ������ʨ��������·һ�ţ�������2007��4��29��.��һ���ɶ����й�����Ԫ�أ��ɵ������ܡ����Ķ��ǡ�����ͼ�ڵȶ�����ʽ���й��Ŵ�����Ԫ�ػ�۶��ɣ�����Ũ���ط��Ž�����ɫ����ʽ��¥.�������������½��ij����Ļ�������Ĵ�������֮һ��ͬʱ�������Եķ羰Ҳ����������.ij��ѧ������ȤС��Ϊ�˲�������ɽ��![]() �ϵ�������
�ϵ�������![]() �ĸ߶ȣ���ɽ���µĹ㳡��
�ĸ߶ȣ���ɽ���µĹ㳡��![]() ����ý������
����ý������![]() ����ɽ����������Ϊ20�㣬��ˮƽ����ǰ��20����
����ɽ����������Ϊ20�㣬��ˮƽ����ǰ��20����![]() �㣬��ý����ﶥ��
�㣬��ý����ﶥ��![]() �������Ϊ45�㣬��֪ɽ��
�������Ϊ45�㣬��֪ɽ��![]() ��37.69��.�����ĸ߶�
��37.69��.�����ĸ߶�![]() .�������ȷ��1�ף��ο����ݣ�
.�������ȷ��1�ף��ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com