
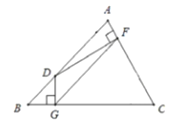
【题目】已知:△ABC中,∠B=45°,∠C=60°,BC=4,D、F分别为AB、AC边上的一个动点,过D分别作DF⊥AC于F,DG⊥BC于G,那么FG的最小值为()
A.2B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
连接CD,利用90°圆周角所对的弦是直径可得点D,G,C,F四点共圆,且CD是圆的直径,当FG⊥CD时,FG最小,利用垂径定理可得CD平分∠ACB,然后设DG=BG=x,则CG=4-x,然后利用三角函数求得x的值,从而求得GF的长度.
解:如图,连接CD.
由题意可知:∠DGC=∠DFC=90°
∴点D,G,C,F四点共圆,且CD是圆的直径,
当FG⊥CD时,FG最小,
∵FG⊥CD
∴直径CD垂直平分FG
又∵∠ACB=60°
△ABC为等边三角形
∴GF=CG
∵∠B=45°,∠DGC =90°
∴设DG=BG=x,则CG=4-x,
在Rt△DCG中,∠GCD=30°
∴![]() ,即
,即![]()
解得:![]()
∴GF=GC=4-x=![]()
故选:C.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为
为![]() 上一点,经过点
上一点,经过点![]() ,
,![]() 的
的![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,连接
,连接![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
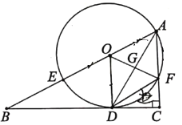
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() ,
,![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两种客车,2辆甲种客车与3辆乙种客车的总载客量为180人,1辆甲种客车与2辆乙种客车的总载客量为105人.
(1)请问1辆甲种客车与1辆乙种客车的载客量分别为多少人?
(2)某学校组织240名师生集体外出活动,拟租用甲、乙两种客车共6辆,一次将全部师生送到指定地点.若每辆甲种客车的租金为400元,每辆乙种客车的租金为280元,请给出最节省费用的租车方案,并求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
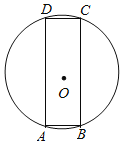
【题目】如图,四边形ABCD是⊙O的内接矩形,将矩形ABCD沿着直线BC翻折,点A、点D的对应点分别为A′、D′,如果直线A′D′与⊙O相切,那么![]() 的值为_____.
的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
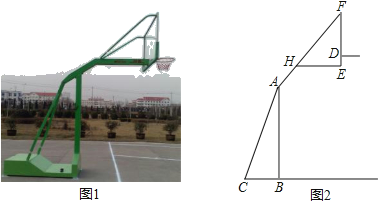
【题目】如图1,2分别是某款篮球架的实物图与示意图,AB⊥BC于点B,底座BC=1.3米,底座BC与支架AC所成的角∠ACB=60°,点H在支架AF上,篮板底部支架EH∥BC.EF⊥EH于点E,已知AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求篮板底部支架HE与支架AF所成的∠FHE的度数.
(2)求篮板底部点E到地面的距离,(精确到0.01米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
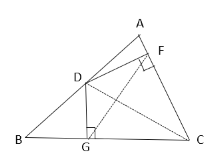
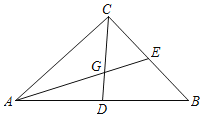
【题目】已知:如图,在Rt△ABC中,∠ACB=90°,BC=12,cosB=![]() ,D、E分别是AB、BC边上的中点,AE与CD相交于点G.
,D、E分别是AB、BC边上的中点,AE与CD相交于点G.
(1)求CG的长;
(2)求tan∠BAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com