
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН![]() x+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпyЃНЉ
x+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЌХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсе§АыжсНЛгкЕуCЃЌСЌНгBCЃЌPЮЊЯпЖЮACЩЯЕФЖЏЕуЃЌPгыAЃЌCВЛжиКЯЃЌзїPQЁЮBCНЛABгкЕуQЃЌAЙигкPQЕФЖдГЦЕуЮЊDЃЌСЌНгPDЃЌQDЃЌBDЃЎ
x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсе§АыжсНЛгкЕуCЃЌСЌНгBCЃЌPЮЊЯпЖЮACЩЯЕФЖЏЕуЃЌPгыAЃЌCВЛжиКЯЃЌзїPQЁЮBCНЛABгкЕуQЃЌAЙигкPQЕФЖдГЦЕуЮЊDЃЌСЌНгPDЃЌQDЃЌBDЃЎ
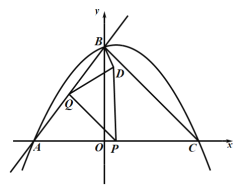
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуDдкХзЮяЯпЩЯЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈ3ЃЉЩшЕуPЕФКсзјБъЮЊxЃЌЁїPDQгыЁїABCЕФжиЕўВПЗжЕФУцЛ§ЮЊS
ЂйжБНгаДГіSгыxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкЕБЁїBDQЮЊжБНЧШ§НЧаЮЪБЃЌжБНгаДГіxЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНЉ![]() x2+
x2+![]() x+4ЃЛЃЈ2ЃЉЕуPЕФзјБъЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉЂйЕБ
x+4ЃЛЃЈ2ЃЉЕуPЕФзјБъЃЈ1ЃЌ0ЃЉЃЛЃЈ3ЃЉЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌЂкЕБ
ЃЌЂкЕБ![]() ЮЊжБНЧШ§НЧаЮЪБЃЌxЕФжЕЪЧ
ЮЊжБНЧШ§НЧаЮЪБЃЌxЕФжЕЪЧ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнвЛДЮКЏЪ§НтЮіЪНЧѓЕУAЃЌBСНЕузјБъЃЌШЛКѓДњШыЕНЖўДЮКЏЪ§НтЮіЪНжаЃЌгУД§ЖЈЯЕЪ§ЗЈЧѓКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуPЕФзјБъЃЈxЃЌ0ЃЉЃЌгЩХзЮяЯпНтЮіЪНЧѓЕУCЕузјБъЃЌгЩДЫЧѓЕУЁЯBCO=45ЁуЃЌгЩЦНааЯпЕФКЭЖдГЦЕФаджЪЧѓЕУЁЯQPA=ЁЯBCO=45ЁуЃЌЁЯAPD=90ЁуЃЌДгЖјЕУЕНЕуDЕФзјБъЃЈxЃЌx+3ЃЉЃЌШЛКѓИљОнЕуDдкХзЮяЯпЩЯСаЗНГЬЧѓНтЃЛ
ЃЈ3ЃЉЂйДцдк2жжЧщПіЃЌвЛжжЪЧЕуDдкBCЕФзѓВрЃЌСэвЛжжЪЧЕуDдкBCЕФгвВрЃЌРћгУШ§НЧаЮЯрЫЦгыУцЛ§ЕФЙиЯЕПЩЧѓЕУЃЛ
ЂкЗжЕБЁЯQBD=90ЁуКЭЁЯQDB=90ЁуСНжжЧщПіЃЌНсКЯЙДЙЩЖЈРэМАЦНааЯпЗжЯпЖЮГЩБШР§ЖЈРэЧѓНтAPЕФГЄЃЌДгЖјЧѓxЕФжЕЃЎ
НтЃКЃЈ1ЃЉдкyЃН![]() x+4жаЃЌСюx=0дђy=4ЃЌСюy=0дђx=-3
x+4жаЃЌСюx=0дђy=4ЃЌСюy=0дђx=-3
ЁрAЃЈ-3ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉ
ЁпХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§AЃЌBСНЕу
x2+bx+cОЙ§AЃЌBСНЕу
Ёр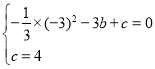
НтЕУ![]()
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНЉ![]() x2+
x2+![]() x+4
x+4
ЃЈ2ЃЉЩшЕуPЕФзјБъЃЈxЃЌ0ЃЉ
СюyЃНЉ![]() x2+
x2+![]() x+4=0
x+4=0
НтЕУ![]() ЃЌ
ЃЌ ![]()
ЫљвдCЃЈ4ЃЌ0ЃЉ
ЁрOB=OC=4
гжЁп PQЁЮBCЧвЕуAЙигкPQЕФЖдГЦЕуЮЊDЃЌ
ЁрЁЯQPA=ЁЯDPQ=ЁЯBCO=45Ёу
ЁрЁЯAPD=90Ёу
гжЁпAЃЈ-3ЃЌ0ЃЉ
ЁрЕуDЕФзјБъЃЈxЃЌx+3ЃЉ,
гЩЬтвтЕуDдкХзЮяЯпЩЯ
Ёрx+3=Љ![]() x2+
x2+![]() x+4
x+4
НтЕУ![]()
![]()
ЁпPгыAЃЌCВЛжиКЯ
ЁрЕуPЕФзјБъЃЈ1ЃЌ0ЃЉЃЎ
ЂйЕБЕуDИеКУдкBCЩЯЪБ
ЁпB(0ЃЌ4)ЃЌC(4ЃЌ0)
ЁржБЯпBCЕФНтЮіЪНЮЊЃКy=-x+4
ЕБЕуDИеКУдкBCЩЯЪБЃЌдђD(xЃЌ-x+4)
ЁпPD=AP
Ёр-x+4=3+xЃЌНтЕУЃКx=![]()
ЧщПівЛЃКЕБЕуDдкжБЯпBCЕФзѓВрЪБЃЌМДЕБ![]() ЪБЃЌЭМаЮШчЯТЃК
ЪБЃЌЭМаЮШчЯТЃК
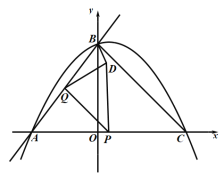
дђ![]()
ЁпA(-3ЃЌ0)ЃЌB(0ЃЌ4)ЃЌC(4ЃЌ0)
Ёр![]()
ЁпQPЁЮBC
ЁрЁЯAQP=ЁЯABC
ЁпЁЯQAP=ЁЯBAC
ЁрЁїAQPЁзЁїABC
Ёр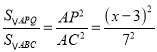
НтЕУЃК![]()
![]() ЃЌМД
ЃЌМД![]()
ЧщПіЖўЃКЕБЕуDдкжБЯпBCЕФгвВрЪБЃЌМДЕБ![]() ЪБЃЌЭМаЮШчЯТЃЌQDНЛBCгкЕуFЃЌDPНЛBCгкЕуEЃК
ЪБЃЌЭМаЮШчЯТЃЌQDНЛBCгкЕуFЃЌDPНЛBCгкЕуEЃК
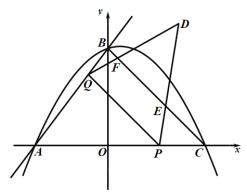
дђ![]()
вбЧѓГі![]()
![]()
ЁпЁЯBCO=45ЁуЃЌЁрЁЯQPA=ЁЯQPD=45Ёу
ЁрЁЯAPD=90ЁуЃЌМДDPЁЭxжс
ЁрЁїPECЪЧЕШбќжБНЧШ§НЧаЮ
ЁрPE=PC=4-x
ЁпAP=x+3ЃЌЁрPD=x+3
ЁрED=DP-PE=2x-1
ЭЌРэПЩжЊЃЌ![]() ЁзЁїABC
ЁзЁїABC
Ёр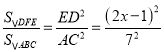
НтЕУЃК![]()
![]()
Ёр![]()
![]() -(
-(![]() )=
)=![]()
МДЃК![]()
злЩЯЕУЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
ЂкШчЭМЃЌСЌНгADЃЌгЩЖдГЦадПЩжЊADЁЭPQ
ЁрЕуDБидкЙ§ЕуAзїBCЕФДЙЯпЩЯЃЌЩшДЙзуЮЊE
ЁрPQЁЮBC
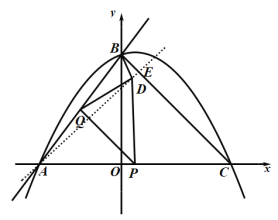
ЕБЁЯQBD=90ЁуЪБЃЌ![]()
Ёр![]()
![]() ЃЌМД
ЃЌМД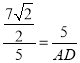
НтЕУЃК![]() ЃЌдђAF=
ЃЌдђAF=![]()
Ёр![]()
Ёр![]() ЃЌМД
ЃЌМД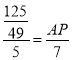
НтЕУЃК![]()
Ёр![]()
ЕБЁЯBDQ=90ЁуЪБЃЌгЩЩЯПЩжЊЃК![]() ЃЌ
ЃЌ![]()
ЁрИљОнЙДЙЩЖЈРэПЩЕУ![]()
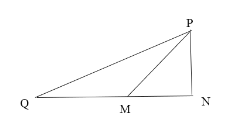
ШчЭМЃЌШєPQ=5ЃЌQN=![]() ЃЌ
ЃЌ![]()
ЩшQM=MP=aЃЌдђ![]()
ЁргЩЙДЙЩЖЈРэПЩЕУ![]()
НтЕУЃК![]()
Ёр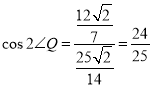
МД![]()
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НтЕУ![]()
Ёр![]()
злЩЯЫљЪіЃЌxЕФжЕЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ


 гХЕШЩњЬтПтЯЕСаД№АИ
гХЕШЩњЬтПтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЮШВНЭЦНј5GЭјТчНЈЩшЃЌЩюЛЏЙВНЈЙВЯэЃЌЕБМзЖгЪЉЙЄ20ЬьЭъГЩ5GЛљеОНЈЩшЙЄГЬЕФ![]() ЪБЃЌввЖгМгШыИУЙЄГЬЃЌНсЙћБШМзЖгЕЅЖРЪЉЙЄЬсЧА25ЬьЭъГЩСЫЪЃгрЕФЙЄГЬЃЎ
ЪБЃЌввЖгМгШыИУЙЄГЬЃЌНсЙћБШМзЖгЕЅЖРЪЉЙЄЬсЧА25ЬьЭъГЩСЫЪЃгрЕФЙЄГЬЃЎ
(1)ШєввЖгЕЅЖРЪЉЙЄЃЌашвЊЖрЩйЬьВХФмЭъГЩИУЯюЙЄГЬЃП
(2)ШєввЖгВЮгыИУЯюЙЄГЬЪЉЙЄЕФЪБМфВЛГЌЙ§12ЬьЃЌдђМзЖгДгПЊЪМЪЉЙЄЕНЭъГЩИУЙЄГЬжСЩйашвЊЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() гыЗДБШР§КЏЪ§
гыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкAЃЈ-1ЃЌ3ЃЉЃЌBЃЈ3ЃЌ
ЕФЭМЯѓНЛгкAЃЈ-1ЃЌ3ЃЉЃЌBЃЈ3ЃЌ![]() ЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
ЃЉСНЕуЃЌЙ§ЕуAзїACЁЭxжсгкЕуCЃЌЙ§ЕуBзїBDЁЭxжсгкЕуDЃЎ
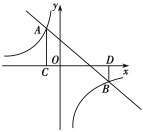
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§МАЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPдкжБЯп![]() ЩЯЃЌЧвSЁїACPЃН2SЁїBDPЃЌЧѓЕуPЕФзјБъЃЎ
ЩЯЃЌЧвSЁїACPЃН2SЁїBDPЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
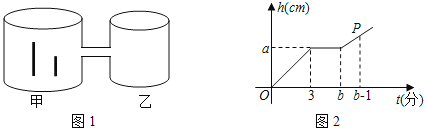
ЁОЬтФПЁПШчЭМ1ЪЧСНдВжљаЮСЌЭЈШнЦїЃЌСНИљЬњАєжБСЂгкМзШнЦїЕзВПЃЈСЌЭЈДІМАЬњАєЬхЛ§КіТдВЛМЦЃЉЃЌЯђМзШнЦїдШЫйзЂЫЎЃЌМзШнЦїЕФЫЎУцИпЖШhЃЈcmЃЉгыЪБМфtЃЈЗжЃЉЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЎвбжЊСНИљЬњАєЕФГЄЖШжЎКЭЮЊ34cmЃЌЕБЫЎУцДяЕНСЌЭЈДІЪБЃЌвЛИљТЖГіЫЎУцЕФГЄЖШЪЧЫќЕФ![]() ЃЌСэвЛИљТЖГіЫЎУцЕФГЄЖШЪЧЫќЕФ
ЃЌСэвЛИљТЖГіЫЎУцЕФГЄЖШЪЧЫќЕФ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЂйЭМ2жаЃЈ3ЃЌaЃЉБэЪОЕФЪЕМЪвтвхЪЧЁЁ ЁЁЃЛ
ЂкЧыЧѓГіaЕФжЕЃЛ
ЃЈ2ЃЉШєМзЁЂввСНШнЦїЕФЕзУцЛ§жЎБШЮЊSМзЃЌSввЃН3ЃК2ЃЎ
ЂйжБНгаДГіbЕФжЕЮЊЁЁ ЁЁЃЛ
ЂкЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНжжПЭГЕЃЌ2СОМзжжПЭГЕгы3СОввжжПЭГЕЕФзмдиПЭСПЮЊ180ШЫЃЌ1СОМзжжПЭГЕгы2СОввжжПЭГЕЕФзмдиПЭСПЮЊ105ШЫЃЎ
ЃЈ1ЃЉЧыЮЪ1СОМзжжПЭГЕгы1СОввжжПЭГЕЕФдиПЭСПЗжБ№ЮЊЖрЩйШЫЃП
ЃЈ2ЃЉФГбЇаЃзщжЏ240УћЪІЩњМЏЬхЭтГіЛюЖЏЃЌФтзтгУМзЁЂввСНжжПЭГЕЙВ6СОЃЌвЛДЮНЋШЋВПЪІЩњЫЭЕНжИЖЈЕиЕуЃЎШєУПСОМзжжПЭГЕЕФзтН№ЮЊ400дЊЃЌУПСОввжжПЭГЕЕФзтН№ЮЊ280дЊЃЌЧыИјГізюНкЪЁЗбгУЕФзтГЕЗНАИЃЌВЂЧѓГізюЕЭЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаМзЁЂввСНжжПЭГЕЃЌ2СОМзжжПЭГЕгы3СОввжжПЭГЕЕФзмдиПЭСПЮЊ180ШЫЃЌ1СОМзжжПЭГЕгы2СОввжжПЭГЕЕФзмдиПЭСПЮЊ105ШЫЃЎ
ЃЈ1ЃЉЧыЮЪ1СОМзжжПЭГЕгы1СОввжжПЭГЕЕФдиПЭСПЗжБ№ЮЊЖрЩйШЫЃП
ЃЈ2ЃЉФГбЇаЃзщжЏ240УћЪІЩњМЏЬхЭтГіЛюЖЏЃЌФтзтгУМзЁЂввСНжжПЭГЕЙВ6СОЃЌвЛДЮНЋШЋВПЪІЩњЫЭЕНжИЖЈЕиЕуЃЎШєУПСОМзжжПЭГЕЕФзтН№ЮЊ400дЊЃЌУПСОввжжПЭГЕЕФзтН№ЮЊ280дЊЃЌЧыИјГізюНкЪЁЗбгУЕФзтГЕЗНАИЃЌВЂЧѓГізюЕЭЗбгУЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ФкЃЌЧв
ФкЃЌЧв![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЃЌЗжБ№НЛ
ЃЌЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гкЕу
гкЕу![]() ЁЂ
ЁЂ![]() ЃЌШє
ЃЌШє![]() гы
гы![]() ЯрЫЦЃЌдђЯпЖЮ
ЯрЫЦЃЌдђЯпЖЮ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
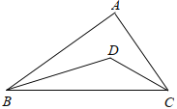
A.5B.![]() C.5Лђ
C.5Лђ![]() D.6
D.6
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
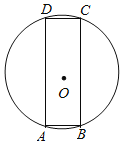
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧЁбOЕФФкНгОиаЮЃЌНЋОиаЮABCDбизХжБЯпBCЗелЃЌЕуAЁЂЕуDЕФЖдгІЕуЗжБ№ЮЊAЁфЁЂDЁфЃЌШчЙћжБЯпAЁфDЁфгыЁбOЯрЧаЃЌФЧУД![]() ЕФжЕЮЊ_____ЃЎ
ЕФжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНаЃИїбЁХЩ10УћбЇЩњВЮМгЁАУРРіЬЉжнЯчЭСЗчЧщжЊЪЖЁБДѓШќдЄШќЃЎИїВЮШќбЁЪжЕФГЩМЈШчЯТЃК
МзаЃЃК93ЃЌ98ЃЌ89ЃЌ93ЃЌ 95ЃЌ96ЃЌ 93ЃЌ96ЃЌ98ЃЌ 99ЃЛ
вваЃЃК93ЃЌ94ЃЌ88ЃЌ91ЃЌ92ЃЌ93ЃЌ100ЃЌ 98ЃЌ98ЃЌ93ЃЎ
ЭЈЙ§ећРэЃЌЕУЕНЪ§ОнЗжЮіБэШчЯТЃК
бЇаЃ | зюИпЗж | ЦНОљЗж | жаЮЛЪ§ | жкЪ§ | ЗНВю |
МзаЃ | 99 | a | 95.5 | 93 | 8.4 |
вваЃ | 100 | 94 | b | 93 | c |
ЃЈ1ЃЉЬюПеЃКa = ЃЌb = ЃЛ
ЃЈ2ЃЉЧѓГіБэжаcЕФжЕЃЌФуШЯЮЊФФЫљбЇаЃДњБэЖгГЩМЈКУЃПЧыаДГіСНЬѕФуШЯЮЊИУЖгГЩМЈКУЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com