
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
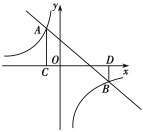
(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
科目:初中数学 来源: 题型:
【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
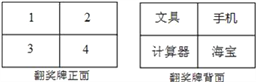
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
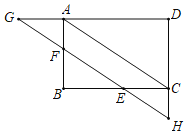
【题目】已知:如图,在矩形ABCD中,E是边BC上一点,过点E作对角线AC的平行线,交AB于F,交DA和DC的延长线于点G,H.
(1)求证:△AFG≌△CHE;
(2)若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中考让同学们感觉压力较大,初三某班班主任想通过课间播放音乐来帮助学生缓解压力,采用全面调查的方法调查了学生对音乐类型的兴趣爱好,结果全班学生选择集中在流行音乐、民族音乐、摇滚音乐和轻音乐四种音乐类型.根据调查的结果绘制成如图所示的两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
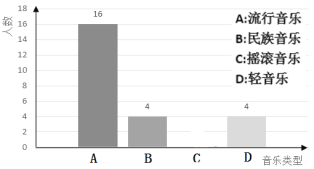
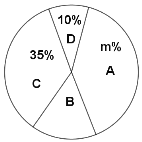
(1)求该班学生总人数,并把条形统计图补充完整;
(2)求扇形统计图中![]() 的值和表示流行音乐的扇形圆心角的度数;
的值和表示流行音乐的扇形圆心角的度数;
(3)班主任每天挑选出四种类型音乐各一首放在一个播放器内,每次随机播放两首不同音乐,请用画树状图或列表的方法求出某次恰好播放民族音乐和轻音乐的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com