
【题目】如图,△ABC中,AB=8,AC=2,∠BAC的外角平分线交BC延长线于点E,BD⊥AE于D,若AE=AC,则AD的长为______.
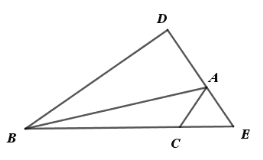
【答案】3
【解析】
延长AD至点G,使DG=AD,连接BG,延长BA至F,根据垂直平分线的性质可得BA=BG=8,然后根据等边对等角、角平分线的定义和平行线的判定证出AC∥GB,从而得出∠ACE=∠GBE,再根据等边对等角和等角对等边可证GB=GE=8,最后根据DG+AD=GE-AE即可求出结论.
解:延长AD至点G,使DG=AD,连接BG,延长BA至F
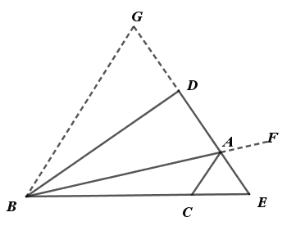
∴BD垂直平分AG
∴BA=BG=8
∴∠BAG=∠G
∵∠BAG=∠EAF,∠BAC的外角平分线交BC延长线于点E,
∴∠EAF=∠G,∠CAE=∠EAF,
∴∠G=∠CAE
∴AC∥GB
∴∠ACE=∠GBE
∵AE=AC=2
∴∠ACE=∠E
∴∠GBE=∠E
∴GB=GE=8
∵DG+AD=GE-AE
∴2AD=6
∴AD=3
故答案为3.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
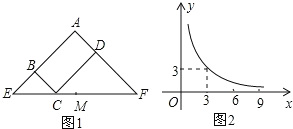
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的序号是___.①当x=3时,EC<EM;②当y=9时,EC>EM③当x增大时,ECCF的值增大;④当y增大时,BEDF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
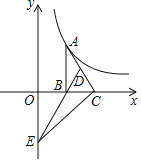
【题目】如图,已知点A在反比例函数y=![]() (x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
(x>0)的图象上,作Rt△ABC,边BC在x轴上,点D为斜边AC的中点,连结DB并延长交y轴于点E,若△BCE的面积为4,则k=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知,在![]() 中,
中,![]() ,求作
,求作![]() 的内心
的内心![]() ,以下甲乙两同学的做法:
,以下甲乙两同学的做法:
甲:如图1
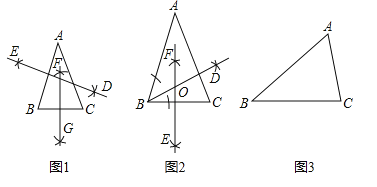
①作![]() 垂直平分线
垂直平分线![]()
②作![]() 的垂直平分线
的垂直平分线![]()
③![]() 交于点
交于点![]()
则点![]() 即为所求
即为所求
乙:如图2
①作![]() 的角平分线
的角平分线![]()
②作![]() 的垂直平分线EF
的垂直平分线EF
③![]() 交于点
交于点![]()
则点![]() 即为所求
即为所求
甲同学的做法__________;乙同学的做法__________(填写正确或不正确)
(2)如图3![]() 中,
中, ![]() ,
,
①用直尺和圆规在![]() 的内部作射线
的内部作射线![]() ,使
,使![]() (不写作法,保留痕迹)
(不写作法,保留痕迹)
②若①中的射线![]() 交
交![]() 于点
于点![]() ,求
,求![]() 的长
的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列有规律的算式:13=1,13+23=9,13+23+33=36,13+23+33+43=100,13+23+33+43+53=225,…,探究并运用其规律计算:113+123+133+143+153+163+173+183+193+203的结果可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
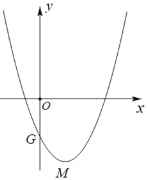
【题目】已知抛物线![]() :
:![]() (m>0)的顶点为M,交y轴于点G.
(m>0)的顶点为M,交y轴于点G.
(1)如图,若点G坐标为(0,![]() )
)
①直接写出抛物线![]() 解析式;
解析式;
②点Q在y轴上,将线段QM绕点Q逆时针旋转90°得线段QN,若点N恰好落在抛物线![]() 上,求点Q的坐标.
上,求点Q的坐标.
(2) 探究: 将抛物线![]() 沿唯一的定直线x=a对称得抛物线
沿唯一的定直线x=a对称得抛物线![]() ,记抛物线
,记抛物线![]() 交y轴于点P (0,-2m),求a的值.
交y轴于点P (0,-2m),求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
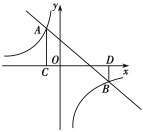
(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
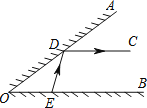
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
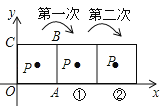
【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com