
【题目】观察下列有规律的算式:13=1,13+23=9,13+23+33=36,13+23+33+43=100,13+23+33+43+53=225,…,探究并运用其规律计算:113+123+133+143+153+163+173+183+193+203的结果可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
找出已知等式的运算规律,并归纳公式,然后先求出13+23+33+……+113+123+133+143+153+163+173+183+193+203的值,再求出13+23+33+……103的值,最后两式相减并利用平方差公式化简即可.
解:13=1,
13+23=9=(1+2)2,
13+23+33=36=(1+2+3)2,
13+23+33+43=100=(1+2+3+4)2,
13+23+33+43+53=225=(1+2+3+4+5)2,
∴13+23+33+……+n3=(1+2+3+……+n)2=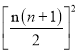 ,
,
∴13+23+33+……+113+123+133+143+153+163+173+183+193+203=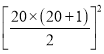 =2102①
=2102①
而13+23+33+……103=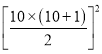 =552②
=552②
∴①-②,得
113+123+133+143+153+163+173+183+193+203=2102-552=(210+55)×(210-55)=265×155
故选A.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)如图,点E,F分别在正方形ABCD的边BC,CD上,连接EF.因为AB=AD,所以把ΔABE绕A逆时针旋转90°至ΔADG,可使AB与AD重合.因为∠CDA=∠B=90°,所以∠FDG=180°,所以F、D、G共线.
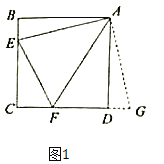
如果__________(填一个条件),可得ΔAEF≌ΔAGF.经过进一步研究我们可以发现:当BE,EF,FD满足__________时,∠EAF=45°.
(应用)
如图,在矩形ABCD中,AB=6,AD=m,点E在边BC上,且BE=2.
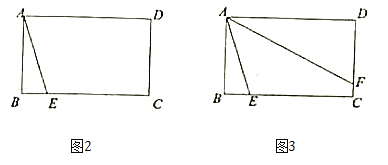
(1)若m=8,点F在边DC上,且∠EAF=45°(如图),求DF的长;
(2)若点F在边DC上,且∠EAF=45°,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
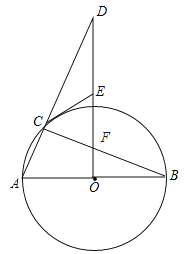
【题目】如图,![]() 是
是![]() 直径,
直径,![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() ,连
,连![]() 接交
接交![]() 于点
于点![]()
(1)求证:![]()
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,填空:
,填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 为正方形;
为正方形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台在它的娱乐性节目中每期抽出两名场外幸运观众,有一期甲、乙两人被抽为场外幸运观众,他们获得了一次抽奖的机会,在如图所示的翻奖牌的正面4个数字中任选一个,选中后翻开,可以得到该数字反面的奖品,第一个人选中的数字第二个人不能再选择了.
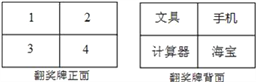
(1)如果甲先抽奖,那么甲获得“手机”的概率是多少?
(2)小亮同学说:甲先抽奖,乙后抽奖,甲、乙两人获得“手机”的概率不同,且甲获得“手机”的概率更大些.你同意小亮同学的说法吗?为什么?请用列表或画树状图分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
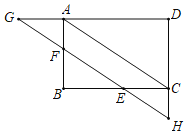
【题目】已知:如图,在矩形ABCD中,E是边BC上一点,过点E作对角线AC的平行线,交AB于F,交DA和DC的延长线于点G,H.
(1)求证:△AFG≌△CHE;
(2)若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要将一份宣传资料进行批量印刷.在甲印刷厂,在收取100元制版费的基础上,每份收费0.5元;在乙印刷厂,在收取40元侧版费的基础上,每份收费0.7元.设该单位要印刷此宣传资料![]() 份(
份(![]() 为正整数).
为正整数).
(Ⅰ)根据题意,填写下表:
印剧数量(份) | 150 | 250 | 350 | 450 | … |
甲印刷厂收费(元) | 175 | ① | 275 | ② | … |
乙印刷厂收费(元) | 145 | 215 | ③ | 355 | … |
(Ⅱ)设在甲印刷厂收费![]() 元,在乙印刷厂收费
元,在乙印刷厂收费![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,在哪家印刷厂花费少?请说明理由.
时,在哪家印刷厂花费少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com