
【题目】如图,![]() 是
是![]() 直径,
直径,![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的切线交
的切线交![]() 于点
于点![]() ,连
,连![]() 接交
接交![]() 于点
于点![]()
(1)求证:![]()
(2)连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,填空:
,填空:
①当![]() 的度数为_________时,四边形
的度数为_________时,四边形![]() 为菱形;
为菱形;
②当![]() 的度数为__________时,四边形
的度数为__________时,四边形![]() 为正方形;
为正方形;
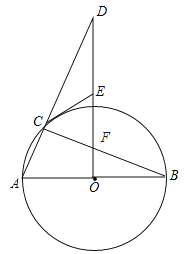
【答案】(1)详见解析;(2)①30°;②22.5°
【解析】
(1)连接OC,利用切线的性质得∠1+∠4=90°,再利用等腰三角形和互余证明∠1=∠2,然后根据等腰三角形的判定定理得到结论;
(2)①当∠D=30°时,∠DAO=60°,证明△CEF和△FEG都为等边三角形,从而得到EF=FG=GE=CE=CF,则可判断四边形ECFG为菱形;
②当∠D=22.5°时,∠DAO=67.5",利用三角形内角和计算出∠COE=45°,利用对称得∠EOG=45°,则∠COG=90°,接着证明△OEC≌△OEG得到∠OGE=∠OCE=90°,从而证明四边形ECOG为矩形,然后进一步证明四边形ECOG为正方形.
(1)证明:连接![]() ,如图:
,如图:
∵![]() 是切线,
是切线,
∴![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
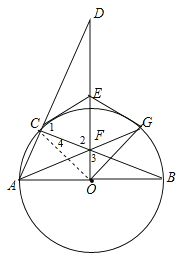
(2)①当∠D=30°吋,∠DAO=60°,
而AB为直径,
∴∠ACB=90°,
∵∠B=30°,
∴∠3=∠2=60°,
而CE=FE,
∴△CEF为等边三角形,
∴CE=CF=EF,
同理可得∠GFE=60°,
利用对称得FG=FC,
∵FG=EF,
∴△FEG为等边三角形,
∴EG=FG,
∴EF=FG=GE=CE,
∴四辺形ECFG为菱形;
故答案为:30°;
②当∠D= 22.5 °时,∠DAO= 67.5°,
而OA=OC,
∴∠OCA=∠OAC=67.5°,
∴∠AOC=180°-67.5°-67.5°=45°,
∴∠AOC=45°,
∴∠COE=45°,
利用对称得∠EOG=45°,
∴∠COG=90°,
易得△OEC≌△OEG,
∴∠OGE=∠OCE=90° ,
∴.四边形ECOG为矩形,
而OC=OG,
∴四边形ECOG为正方形,
故答案为:22.5°.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx﹣3与x轴交于A,B两点,与y轴交于点C,且OB=OC=3OA,求抛物线的解析式( )
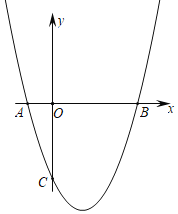
A.y=x2﹣2x﹣3B.y=x2﹣2x+3C.y=x2﹣2x﹣4D.y=x2﹣2x﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学生的学习兴趣如何是每位教师非常关注的问题.为此,某校教师对该校部分学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣);并将调查结果绘制成了图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
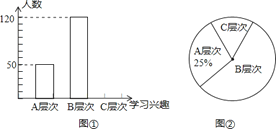
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求图②中C层次所在扇形的圆心角的度数;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣(包括A层次和B层次).
查看答案和解析>>
科目:初中数学 来源: 题型:
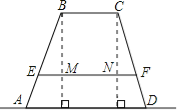
【题目】某高中学校为高一新生设计的学生板凳的正面视图如图所示,其中BA=CD,BC=20cm,BC、EF平行于地面AD且到地面AD的距离分别为40cm、8cm.为使板凳两腿底端A、D之间的距离为50cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
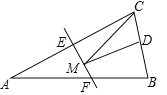
【题目】如图,等腰![]() 的底边
的底边![]() 长为4,面积为12,腰
长为4,面积为12,腰![]() 的垂直平分线
的垂直平分线![]() 分别交边
分别交边![]() 于点
于点![]() ,若点D是的
,若点D是的![]() 中点,点M为线段
中点,点M为线段![]() 上一动点,当
上一动点,当![]() 的周长最小时,
的周长最小时,![]() 长为( )
长为( )
A.1B.3C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列有规律的算式:13=1,13+23=9,13+23+33=36,13+23+33+43=100,13+23+33+43+53=225,…,探究并运用其规律计算:113+123+133+143+153+163+173+183+193+203的结果可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
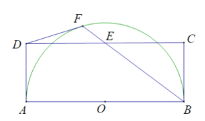
【题目】如图,在矩形ABCD中,边AB是半圆O的直径,点E是CD的中点,BE交半圆O于点F,连接DF.
(1)求证:DF是半圆O的切线;
(2)若AB =8,AD =3,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
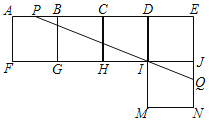
【题目】如图,一“L”型纸片是由5个边长都是10cm的正方形拼接而成,过点I的直线分别与AE,JN交于点P,Q,且“L”型纸片被直线PQ分成面积相等的上下两部分,将该纸片沿BG,CH,DI,IJ折成一个无盖的正方体盒子后,点P,Q之间的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC≤BC,将△ABC沿EF折叠,使点A落在直角边BC上的D点处,设EF与AB、AC边分别交于点E、点F,如果折叠后△CDF与△BDE均为等腰三角形,那么∠B=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com