
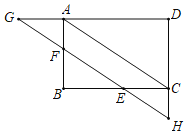
【题目】已知:如图,在矩形ABCD中,E是边BC上一点,过点E作对角线AC的平行线,交AB于F,交DA和DC的延长线于点G,H.
(1)求证:△AFG≌△CHE;
(2)若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.
【答案】(1)见解析;(2)四边形ABCD是正方形,理由见解析
【解析】
(1)根据SAS可以证明两三角形全等;
(2)先根据平行线的性质和已知可得∠BAC=45°,所以△ABC是等腰直角三角形,所以AB=BC,可得结论.
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AB∥CD,∠BAD=∠BCD=90°
∴∠GAB=∠B=∠BCH,
∵AD∥BC,EF∥AC,
∴四边形AGEC是平行四边形,
∴AG=EC,
∵AB∥CD,EF∥AC
∴四边形AFHC是平行四边形,
∴AF=CH,
∴△AFG≌△CHE(SAS).
(2)四边形ABCD是正方形
理由:∵EF∥AC,
∴∠G=∠CAD,
∵∠G=∠BAC,
∴∠BAC=∠CAD,
∵∠BAD=90°,
∴∠BAC=45°,
∵∠B=90°,
∴∠BAC=∠ACB=45°,
∴BA=BC,
∴矩形ABCD是正方形.


科目:初中数学 来源: 题型:
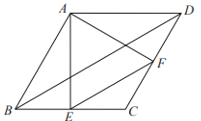
【题目】如图,已知在平行四边形ABCD中,AE⊥BC,垂足为点E,AF⊥CD,垂足为点F.
(1)如果AB=AD,求证:EF∥BD
(2)如果EF∥BD,求证:AB=AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列有规律的算式:13=1,13+23=9,13+23+33=36,13+23+33+43=100,13+23+33+43+53=225,…,探究并运用其规律计算:113+123+133+143+153+163+173+183+193+203的结果可表示为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
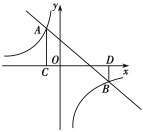
【题目】如图,直线![]() 与反比例函数
与反比例函数![]() 的图象交于A(-1,3),B(3,
的图象交于A(-1,3),B(3,![]() )两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求一次函数及反比例函数的解析式;
(2)若点P在直线![]() 上,且S△ACP=2S△BDP,求点P的坐标.
上,且S△ACP=2S△BDP,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
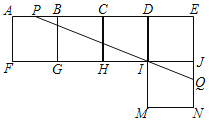
【题目】如图,一“L”型纸片是由5个边长都是10cm的正方形拼接而成,过点I的直线分别与AE,JN交于点P,Q,且“L”型纸片被直线PQ分成面积相等的上下两部分,将该纸片沿BG,CH,DI,IJ折成一个无盖的正方体盒子后,点P,Q之间的距离为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB的一边OA为平面镜,∠AOB=37°36′,在OB上有一点E,从E点射出一束光线经OA上一点D反射,反射光线DC恰好与OB平行,则∠DEB的度数是_____°.
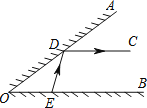
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司生产的一种商品其售价是成本的1.5倍,当售价降低5元时商品的利润率为25%.若不进行任何推广年销售量为1万件.为了获得更好的利益,公司准备拿出一定的资金做推广,根据经验,每年投入的推广费x万元时销售量y(万件)是x的二次函数:当x为1万元时,y是1.5(万件).当x为2万元时,y是1.8(万件).
(1)求该商品每件的的成本与售价分别是多少元?
(2)求出年利润与年推广费x的函数关系式;
(3)如果投入的年推广告费为1万到3万元(包括1万和3万元),问推广费在什么范同内,公司获得的年利润随推广费的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,坐标平面里的图像表示一汽车从甲地到乙地时间x与路程y之间的函数关系,横线表示停车修理.
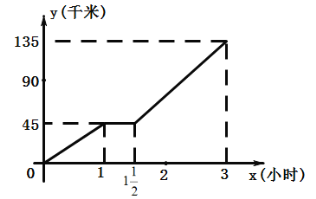
(1)根据图像回答下列问题:前1小时汽车的速度是多少千米/时;停车修理的时间为多少?;后![]() 小时汽车的速度是多少千米/时?甲、乙两地相距多少千米?
小时汽车的速度是多少千米/时?甲、乙两地相距多少千米?
(2)适当选取图像中所给的数据,编一个一元一次方程应用题,并列出方程(不要求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com