
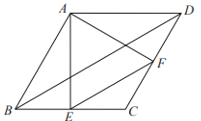
【题目】如图,已知在平行四边形ABCD中,AE⊥BC,垂足为点E,AF⊥CD,垂足为点F.
(1)如果AB=AD,求证:EF∥BD
(2)如果EF∥BD,求证:AB=AD.
【答案】(1)见解析;(2)见解析
【解析】
(1)直接利用平行四边形的性质结合全等三角形的判定方法得出△ABE≌△ADF(AAS),进而求出答案;
(2)利用平行线分线段成比例定理结合相似三角形的判定与性质得出△ABE∽△ADF,进而求出答案.
(1)∵四边形ABCD是平行四边形,
∴∠ABE=∠ADF,BC=AD,AB=CD,
∵AB=AD,
∴BC=AD=AB=CD,
∵AE![]() BC,AF
BC,AF![]() CD,
CD,
∴∠AEB=∠AFD=90,
∵AB=AD,
∴△ABE≌△ADF(AAS),
∴BE=DF,
∴![]() ,
,
∴![]() ,
,
∴EF∥BD.
(2)∵四边形ABCD是平行四边形,
∴∠ABE=∠ADF,
∵AE![]() BC,AF
BC,AF![]() CD,
CD,
∴∠AEB=∠AFD=90,
∴△ABE∽△ADF,
∴![]() ,
,
∵EF∥BD,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴AB=AD.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,O为AC的中点,过点O的直线分别与AB,CD交于点E,F,连接BF交AC于点M,连接DE,BO.若∠COB=60°,FO=FC,则下列结论:①FB⊥OC,OM=CM;②△EOB≌△CMB;③四边形EBFD是菱形;④MB∶OE=3∶2.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量路灯(OS)的高度,把一根长1.5米的竹竿(AB)竖直立在水平地面上,测得竹竿的影子(BC)长为1米,然后拿竹竿向远离路灯方向走了4米(BB′),再把竹竿竖立在地面上,测得竹竿的影长(B′C′)为1.8米,求路灯离地面的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
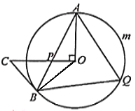
【题目】如图,AB是⊙O的弦,过点O作OC⊥OA,OC交于AB于P,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)已知∠BAO=25°,点Q是弧AmB上的一点.
①求∠AQB的度数;
②若OA=18,求弧AmB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办中学生足球赛,初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛,六支球队分成甲、乙两组,甲组由A、e、f三队组成,乙组由B、g、h三队组成,现要从甲、乙两组中各随机抽取一支球队进行首场比赛.
(1)在甲组中,首场比赛抽到e队的概率是 ;
(2)请你用画树状图或列表的方法,求首场比赛出场的两个队都是县区学校队的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(发现)如图,点E,F分别在正方形ABCD的边BC,CD上,连接EF.因为AB=AD,所以把ΔABE绕A逆时针旋转90°至ΔADG,可使AB与AD重合.因为∠CDA=∠B=90°,所以∠FDG=180°,所以F、D、G共线.
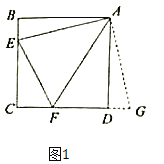
如果__________(填一个条件),可得ΔAEF≌ΔAGF.经过进一步研究我们可以发现:当BE,EF,FD满足__________时,∠EAF=45°.
(应用)
如图,在矩形ABCD中,AB=6,AD=m,点E在边BC上,且BE=2.
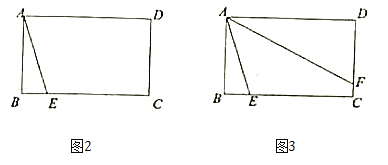
(1)若m=8,点F在边DC上,且∠EAF=45°(如图),求DF的长;
(2)若点F在边DC上,且∠EAF=45°,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
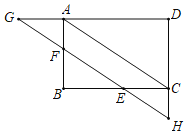
【题目】已知:如图,在矩形ABCD中,E是边BC上一点,过点E作对角线AC的平行线,交AB于F,交DA和DC的延长线于点G,H.
(1)求证:△AFG≌△CHE;
(2)若∠G=∠BAC,则四边形ABCD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com