
ЁОЬтФПЁПФГЙЋЫОЩњВњЕФвЛжжЩЬЦЗЦфЪлМлЪЧГЩБОЕФ1.5БЖЃЌЕБЪлМлНЕЕЭ5дЊЪБЩЬЦЗЕФРћШѓТЪЮЊ25%ЃЎШєВЛНјааШЮКЮЭЦЙуФъЯњЪлСПЮЊ1ЭђМўЃЎЮЊСЫЛёЕУИќКУЕФРћвцЃЌЙЋЫОзМБИФУГівЛЖЈЕФзЪН№зіЭЦЙуЃЌИљОнОбщЃЌУПФъЭЖШыЕФЭЦЙуЗбxЭђдЊЪБЯњЪлСПyЃЈЭђМўЃЉЪЧxЕФЖўДЮКЏЪ§ЃКЕБxЮЊ1ЭђдЊЪБЃЌyЪЧ1.5ЃЈЭђМўЃЉЃЎЕБxЮЊ2ЭђдЊЪБЃЌyЪЧ1.8ЃЈЭђМўЃЉЃЎ
ЃЈ1ЃЉЧѓИУЩЬЦЗУПМўЕФЕФГЩБОгыЪлМлЗжБ№ЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЧѓГіФъРћШѓгыФъЭЦЙуЗбxЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЙћЭЖШыЕФФъЭЦЙуИцЗбЮЊ1ЭђЕН3ЭђдЊЃЈАќРЈ1ЭђКЭ3ЭђдЊЃЉЃЌЮЪЭЦЙуЗбдкЪВУДЗЖЭЌФкЃЌЙЋЫОЛёЕУЕФФъРћШѓЫцЭЦЙуЗбЕФдіДѓЖјдіДѓЃП
ЁОД№АИЁПЃЈ1ЃЉИУЩЬЦЗУПМўЕФЕФГЩБОгыЪлМлЗжБ№ЪЧ20дЊЁЂ30дЊЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЭЦЙуЗбдк1ЭђдЊЕН2ЃЎ5ЭђдЊЃЈАќРЈ1ЭђдЊКЭ2ЃЎ5ЭђдЊЃЉЪБЃЌЙЋЫОЛёЕУЕФФъРћШѓЫцЭЦЙуЗбЕФдіДѓЖјдіДѓЃЎ
ЃЛЃЈ3ЃЉЭЦЙуЗбдк1ЭђдЊЕН2ЃЎ5ЭђдЊЃЈАќРЈ1ЭђдЊКЭ2ЃЎ5ЭђдЊЃЉЪБЃЌЙЋЫОЛёЕУЕФФъРћШѓЫцЭЦЙуЗбЕФдіДѓЖјдіДѓЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЪлМлГЩБОМлЃНРћШѓЃЌГЩБОМлГЫвдРћШѓТЪЃНРћШѓЃЌСаЗНГЬМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнУПФъЭЖШыЕФЭЦЙуЗбxЭђдЊЪБЯњЪлСПyЃЈЭђМўЃЉЪЧxЕФЖўДЮКЏЪ§ЃЌДњШыЫљИјЪ§ОнМДПЩЧѓНтЃЛ
ЃЈ3ЃЉИљОнФъРћШѓЃНЕЅМўРћШѓГЫвдЯњЪлСПдйМѕШЅЭЦЙуЗбМДПЩСаГіЖўДЮКЏЪ§ЃЌИљОнЖўДЮКЏЪ§ЕФаджЪМДПЩШЗЖЈЭЦЙуЗбЕФШЁжЕЗЖЮЇЃЎ
ЃЈ1ЃЉЩшИУЩЬЦЗУПМўЕФЕФГЩБОЮЊaдЊЃЌдђЪлМлЮЊдЊ1.5aдЊЃЌ
ИљОнЬтвтЃЌЕУ
1.5aЉ5ЉaЃН25%aЃЌ
НтЕУaЃН20ЃЌдђ1.5aЃН30ЃЌ
Д№ЃКИУЩЬЦЗУПМўЕФЕФГЩБОгыЪлМлЗжБ№ЪЧ20дЊЁЂ30дЊЃЎ
ЃЈ2ЃЉИљОнЬтвтУПФъЭЖШыЕФЭЦЙуЗбxЭђдЊЪБЯњЪлСПyЃЈЭђМўЃЉЪЧxЕФЖўДЮКЏЪ§ЃЌ
ЩшyЃНax2+bx+c
ЁпВЛНјааШЮКЮЭЦЙуФъЯњЪлСПЮЊ1ЭђМўЃЌМДЕБxЃН0ЪБЃЌyЃН1ЃЈЭђМўЃЉЃЌ
ЕБxЮЊ1ЭђдЊЪБЃЌyЪЧ1.5ЃЈЭђМўЃЉЃЎЕБxЮЊ2ЭђдЊЪБЃЌyЪЧ1.8ЃЈЭђМўЃЉЃЎ
Ёр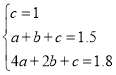
НтЕУ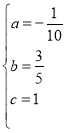
ЫљвдЯњЪлСПyгыЭЦЙуЗбxЕФКЏЪ§НтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЫљвдЩшЙЋЫОЛёЕУЕФФъРћШѓЮЊwЭђдЊЃЌ
Д№ЃКФъРћШѓгыФъЭЦЙуЗбxЕФКЏЪ§ЙиЯЕЪНЮЊwЃН10yЃНЉx2+6x+10ЃЎ
ЃЈ3ЃЉЙЋЫОЛёЕУЕФФъРћШѓЮЊwЭђдЊЃЌИљОнЬтвтЃЌЕУ
wЃН10yЉx
ЃН10ЃЈЉ![]() x2+
x2+![]() x+1ЃЉЉx
x+1ЃЉЉx
ЃНЉx2+5x+10
ЃНЉЃЈxЉ![]() ЃЉ2+
ЃЉ2+![]()
Ёп1ЁмxЁм3ЃЌ
ЁрЕБ1ЁмxЁм2.5ЪБЃЌwЫцxЕФдіДѓЖјдіДѓЃЌ
Д№ЃКЭЦЙуЗбдк1ЭђдЊЕН2.5ЭђдЊЃЈАќРЈ1ЭђдЊКЭ2.5ЭђдЊЃЉЪБЃЌЙЋЫОЛёЕУЕФФъРћШѓЫцЭЦЙуЗбЕФдіДѓЖјдіДѓЃЎ


 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
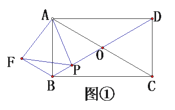
ЁОЬтФПЁПЃЈЗЂЯжЃЉШчЭМЃЌЕуEЃЌFЗжБ№дке§ЗНаЮABCDЕФБпBCЃЌCDЩЯЃЌСЌНгEFЃЎвђЮЊAB=ADЃЌЫљвдАбІЄABEШЦAФцЪБеыа§зЊ90ЁужСІЄADGЃЌПЩЪЙABгыADжиКЯЃЎвђЮЊЁЯCDA=ЁЯB=90ЁуЃЌЫљвдЁЯFDG=180ЁуЃЌЫљвдFЁЂDЁЂGЙВЯпЃЎ
ШчЙћ__________ЃЈЬювЛИіЬѕМўЃЉЃЌПЩЕУІЄAEFЁеІЄAGFЃЎОЙ§НјвЛВНбаОПЮвУЧПЩвдЗЂЯжЃКЕБBEЃЌEFЃЌFDТњзу__________ЪБЃЌЁЯEAF=45ЁуЃЎ
ЃЈгІгУЃЉ
ШчЭМЃЌдкОиаЮABCDжаЃЌAB=6ЃЌAD=mЃЌЕуEдкБпBCЩЯЃЌЧвBE=2ЃЎ
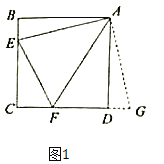
ЃЈ1ЃЉШєm=8ЃЌЕуFдкБпDCЩЯЃЌЧвЁЯEAF=45ЁуЃЈШчЭМЃЉЃЌЧѓDFЕФГЄЃЛ
ЃЈ2ЃЉШєЕуFдкБпDCЩЯЃЌЧвЁЯEAF=45ЁуЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕчЪгЬЈдкЫќЕФгщРжадНкФПжаУПЦкГщГіСНУћГЁЭтавдЫЙлжкЃЌгавЛЦкМзЁЂввСНШЫБЛГщЮЊГЁЭтавдЫЙлжкЃЌЫћУЧЛёЕУСЫвЛДЮГщНБЕФЛњЛсЃЌдкШчЭМЫљЪОЕФЗНБХЦЕФе§Уц4ИіЪ§зжжаШЮбЁвЛИіЃЌбЁжаКѓЗПЊЃЌПЩвдЕУЕНИУЪ§зжЗДУцЕФНБЦЗЃЌЕквЛИіШЫбЁжаЕФЪ§зжЕкЖўИіШЫВЛФмдйбЁдёСЫЃЎ
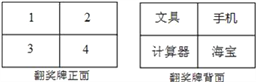
ЃЈ1ЃЉШчЙћМзЯШГщНБЃЌФЧУДМзЛёЕУЁАЪжЛњЁБЕФИХТЪЪЧЖрЩйЃП
ЃЈ2ЃЉаЁССЭЌбЇЫЕЃКМзЯШГщНБЃЌввКѓГщНБЃЌМзЁЂввСНШЫЛёЕУЁАЪжЛњЁБЕФИХТЪВЛЭЌЃЌЧвМзЛёЕУЁАЪжЛњЁБЕФИХТЪИќДѓаЉЃЎФуЭЌвтаЁССЭЌбЇЕФЫЕЗЈТ№ЃПЮЊЪВУДЃПЧыгУСаБэЛђЛЪїзДЭМЗжЮіЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
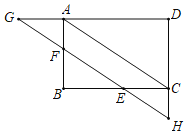
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкОиаЮABCDжаЃЌEЪЧБпBCЩЯвЛЕуЃЌЙ§ЕуEзїЖдНЧЯпACЕФЦНааЯпЃЌНЛABгкFЃЌНЛDAКЭDCЕФбгГЄЯпгкЕуGЃЌHЃЎ
(1)ЧѓжЄЃКЁїAFGЁеЁїCHEЃЛ
(2)ШєЁЯGЃНЁЯBACЃЌдђЫФБпаЮABCDЪЧЪВУДЬиЪтЫФБпаЮЃПВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌABЃН3ЃЌBCЃН4ЃЌНЋЖдНЧЯпACШЦЖдНЧЯпНЛЕуOа§зЊЃЌЗжБ№НЛБпADЁЂBCгкЕуEЁЂFЃЌЕуPЪЧБпDCЩЯЕФвЛИіЖЏЕуЃЌЧвБЃГжDPЃНAEЃЌСЌНгPEЁЂPFЃЌЩшAEЃНxЃЈ0ЃМxЃМ3ЃЉЃЎ
ЃЈ1ЃЉЬюПеЃКPCЃНЁЁ ЁЁЃЌFCЃНЁЁ ЁЁЃЛЃЈгУКЌxЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ2ЃЉЧѓЁїPEFУцЛ§ЕФзюаЁжЕЃЛ
ЃЈ3ЃЉдкдЫЖЏЙ§ГЬжаЃЌPEЁЭPFЪЧЗёГЩСЂЃПШєГЩСЂЃЌЧѓГіxЕФжЕЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаПМШУЭЌбЇУЧИаОѕбЙСІНЯДѓЃЌГѕШ§ФГАрАржїШЮЯыЭЈЙ§ПЮМфВЅЗХвєРжРДАяжњбЇЩњЛКНтбЙСІЃЌВЩгУШЋУцЕїВщЕФЗНЗЈЕїВщСЫбЇЩњЖдвєРжРраЭЕФаЫШЄАЎКУЃЌНсЙћШЋАрбЇЩњбЁдёМЏжадкСїаавєРжЁЂУёзхвєРжЁЂвЁЙівєРжКЭЧсвєРжЫФжжвєРжРраЭЃЎИљОнЕїВщЕФНсЙћЛцжЦГЩШчЭМЫљЪОЕФСНЗљВЛЭъећЕФЭГМЦЭМЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
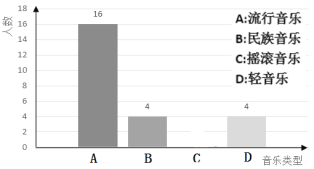
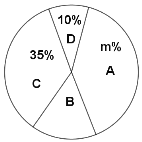
ЃЈ1ЃЉЧѓИУАрбЇЩњзмШЫЪ§ЃЌВЂАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉЧѓЩШаЮЭГМЦЭМжа![]() ЕФжЕКЭБэЪОСїаавєРжЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЕФжЕКЭБэЪОСїаавєРжЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉАржїШЮУПЬьЬєбЁГіЫФжжРраЭвєРжИївЛЪзЗХдквЛИіВЅЗХЦїФкЃЌУПДЮЫцЛњВЅЗХСНЪзВЛЭЌвєРжЃЌЧыгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЧѓГіФГДЮЧЁКУВЅЗХУёзхвєРжКЭЧсвєРжЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
 ЁЁЁЁЁЁ
ЁЁЁЁЁЁ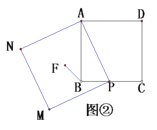 ЁЁЁЁЁЁ
ЁЁЁЁЁЁ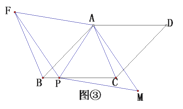
ШчЭМЂйЃЌОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЌЕу
ЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯШЮвтвЛЕуЃЌвд
ЩЯШЮвтвЛЕуЃЌвд![]() ЮЊБпзїЕШБпШ§НЧаЮ
ЮЊБпзїЕШБпШ§НЧаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌдђ
ЃЌдђ![]() гы
гы![]() жЎМфЕФЪ§СПЙиЯЕЪЧ ЃЛ
жЎМфЕФЪ§СПЙиЯЕЪЧ ЃЛ
ЃЈ2ЃЉРрБШбгЩь
ШчЭМЂкЃЌдке§ЗНаЮ![]() жаЃЌЕу
жаЃЌЕу![]() ЮЊ
ЮЊ![]() БпЩЯШЮвтвЛЕуЃЌвд
БпЩЯШЮвтвЛЕуЃЌвд![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЌ
ЃЌ![]() ЮЊе§ЗНаЮ
ЮЊе§ЗНаЮ![]() ЕФжааФЃЌСЌНг
ЕФжааФЃЌСЌНг![]() ЃЌжБНгаДГі
ЃЌжБНгаДГі![]() гы
гы![]() ЕФЪ§СПЙиЯЕЮЊ ЃЛ
ЕФЪ§СПЙиЯЕЮЊ ЃЛ
ЃЈ3ЃЉЭиеЙЧЈвЦ
ШчЭМЂлЃЌдкСтаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() БпЩЯвЛЕуЃЌвд
БпЩЯвЛЕуЃЌвд![]() ЮЊЖдНЧЯпзїСтаЮ
ЮЊЖдНЧЯпзїСтаЮ![]() ЃЌТњзу
ЃЌТњзу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌВТЯы
ЃЌВТЯы![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЕЅЮЛвЊНЋвЛЗнаћДЋзЪСЯНјааХњСПгЁЫЂЃЎдкМзгЁЫЂГЇЃЌдкЪеШЁ100дЊжЦАцЗбЕФЛљДЁЩЯЃЌУПЗнЪеЗб0.5дЊЃЛдкввгЁЫЂГЇЃЌдкЪеШЁ40дЊВрАцЗбЕФЛљДЁЩЯЃЌУПЗнЪеЗб0.7дЊЃЎЩшИУЕЅЮЛвЊгЁЫЂДЫаћДЋзЪСЯ![]() ЗнЃЈ
ЗнЃЈ![]() ЮЊе§ећЪ§ЃЉЃЎ
ЮЊе§ећЪ§ЃЉЃЎ
ЃЈЂёЃЉИљОнЬтвтЃЌЬюаДЯТБэЃК
гЁОчЪ§СПЃЈЗнЃЉ | 150 | 250 | 350 | 450 | Ё |
МзгЁЫЂГЇЪеЗбЃЈдЊЃЉ | 175 | Ђй | 275 | Ђк | Ё |
ввгЁЫЂГЇЪеЗбЃЈдЊЃЉ | 145 | 215 | Ђл | 355 | Ё |
ЃЈЂђЃЉЩшдкМзгЁЫЂГЇЪеЗб![]() дЊЃЌдкввгЁЫЂГЇЪеЗб
дЊЃЌдкввгЁЫЂГЇЪеЗб![]() дЊЃЌЗжБ№аДГі
дЊЃЌЗжБ№аДГі![]() ЃЌ
ЃЌ![]() Йигк
Йигк![]() ЕФКЏЪ§НтЮіЪНЃЛ
ЕФКЏЪ§НтЮіЪНЃЛ
ЃЈЂѓЃЉЕБ![]() ЪБЃЌдкФФМвгЁЫЂГЇЛЈЗбЩйЃПЧыЫЕУїРэгЩЃЎ
ЪБЃЌдкФФМвгЁЫЂГЇЛЈЗбЩйЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
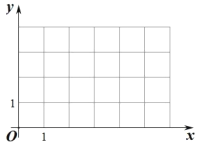
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЮвУЧАбКсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазіећЕуЃЌвбжЊЕу
жаЃЌЮвУЧАбКсЁЂзнзјБъЖМЪЧећЪ§ЕФЕуНазіећЕуЃЌвбжЊЕу![]() ЃЌЕу
ЃЌЕу![]() ЪЧ
ЪЧ![]() жсе§АыжсЩЯЕФЕуЃЌМЧ
жсе§АыжсЩЯЕФЕуЃЌМЧ![]() ФкВП(ВЛАќРЈБпНч)ЕФећЕуИіЪ§ЮЊ
ФкВП(ВЛАќРЈБпНч)ЕФећЕуИіЪ§ЮЊ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ЕФКсзјБъ
ЕФКсзјБъ![]() ЕФШЁжЕЗЖЮЇЪЧ____ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com